ГДЗ по Алгебре 8 Класс Номер 478 Дорофеев, Суворова — Подробные Ответы

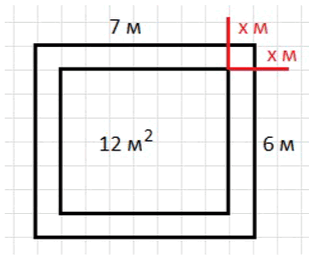
На участке прямоугольной формы со сторонами 7 м и 6 м хотят разместить прямоугольную клумбу площадью 12 м^2 так, чтобы ширина образовавшейся вокруг клумбы дорожки была везде одинаковой. Какую ширину долна иметь дорожка?

Пусть ширина дорожки равна $x$ м, тогда размеры клумбы равны $7 — 2x$ м и $6 — 2x$ м.

Составим уравнение:

$$(7-2x)(6-2x)=12$$

$$(7 — 2x)(6 — 2x) = 12$$ $$42-14x-12x+4x^2-12=0$$

$$42 — 14x — 12x + 4x^2 — 12 = 0$$ $$4x^2-26x+30=0\mathrm{\mid }:2$$

$$4x^2 — 26x + 30 = 0 \quad | : 2$$ $$2x^2-13x+15=0$$

$$2x^2 — 13x + 15 = 0$$ $$D=169-4\cdot 2\cdot 15=169-120=49=\sqrt{49}=7.$$

$$D = 169 — 4 \cdot 2 \cdot 15 = 169 — 120 = 49 = \sqrt{49} = 7.$$ $$x_1=\frac{13-7}{4}=\frac{6}{4}=\frac{3}{2}=1,5(\text{м})\text{— ширина дорожки};$$

$$x_1 = \frac{13 — 7}{4} = \frac{6}{4} = \frac{3}{2} = 1,5 \, (\text{м}) \quad \text{— ширина дорожки};$$ $$x_2 = \frac{13 + 7}{4} = \frac{20}{4} = 5 \quad \text{— не подходит}.$$

Ответ: $1,5$ м.

1. Дано:

Пусть ширина дорожки равна $x$ м, тогда размеры клумбы составляют $7 — 2x$ м и $6 — 2x$ м. Задача заключается в том, чтобы найти ширину дорожки, при этом площадь клумбы должна быть равна 12 м².

2. Составляем уравнение:

Площадь клумбы можно найти по формуле для площади прямоугольника:

$$\text{Площадь клумбы} = \text{длина} \times \text{ширина}$$

Таким образом, площадь клумбы:

$$(7 — 2x)(6 — 2x) = 12$$

3. Раскрываем скобки:

Для упрощения уравнения раскроем скобки:

$$(7 — 2x)(6 — 2x) = 7(6 — 2x) — 2x(6 — 2x)$$ $$= 42 — 14x — 12x + 4x^2$$

Таким образом, получаем:

$$42 — 14x — 12x + 4x^2 = 12$$

4. Упрощаем уравнение:

Теперь соберем все слагаемые на одной стороне и упростим:

$$42 — 26x + 4x^2 = 12$$

Переносим 12 на левую сторону:

$$42 — 26x + 4x^2 — 12 = 0$$

Упрощаем:

$$4x^2 — 26x + 30 = 0$$

5. Делим на 2:

Чтобы упростить коэффициенты, разделим все уравнение на 2:

$$\frac{4x^2}{2} — \frac{26x}{2} + \frac{30}{2} = 0$$

Получаем:

$$2x^2 — 13x + 15 = 0$$

6. Находим дискриминант:

Для решения квадратного уравнения используем формулу дискриминанта:

$$D = b^2 — 4ac$$

где $a = 2$, $b = -13$, $c = 15$.

Подставляем значения:

$$D = (-13)^2 — 4 \cdot 2 \cdot 15 = 169 — 120 = 49$$

Таким образом, $D = 49$, и $\sqrt{49} = 7$.

7. Находим корни уравнения:

Теперь находим корни уравнения с помощью формулы:

$$x = \frac{-b \pm \sqrt{D}}{2a}$$

Подставляем значения:

$$x = \frac{-(-13) \pm \sqrt{49}}{2 \cdot 2} = \frac{13 \pm 7}{4}$$

Таким образом, получаем два корня:

$$x_1 = \frac{13 — 7}{4} = \frac{6}{4} = \frac{3}{2} = 1,5 \, (\text{м}) \quad \text{— ширина дорожки}$$ $$x_2 = \frac{13 + 7}{4} = \frac{20}{4} = 5 \quad \text{— не подходит, так как ширина дорожки не может быть больше, чем половина длины клумбы}$$

8. Ответ:

Ширина дорожки составляет $1,5$ м.

Ответ: $1,5$ м.