ГДЗ по Алгебре 8 Класс Номер 471 Дорофеев, Суворова — Подробные Ответы

Две дороги пересекаются под прямым углом. От перекрестка одновременно отъехали два велосипедиста, один в южном направлении, а другой в восточном. Скорость второго была на 4 км/ч больше скорости первого. Через час расстояние между ними оказалось равным 20 км. Определите скорость каждого велосипедиста.

Пусть скорость первого велосипедиста равна $x$ км/ч, тогда скорость второго велосипедиста равна $x + 4$ км/ч. За один час первый проедет $x$ км, а второй проедет $x + 4$ км.

Составим уравнение, используя теорему Пифагора:

$$x^2+(x+4{)}^2={20}^2$$

$$x^2 + (x + 4)^2 = 20^2$$ $$x^2+x^2+8x+16-400=0$$

$$x^2 + x^2 + 8x + 16 — 400 = 0$$ $$2x^2+8x-384=0\mathrm{\mid }:2$$

$$2x^2 + 8x — 384 = 0 \quad | : 2$$ $$x^2+4x-192=0$$

$$x^2 + 4x — 192 = 0$$ $$D=4^2+4\cdot 1\cdot 192=16+768=784=\sqrt{784}=28.$$

$$D = 4^2 + 4 \cdot 1 \cdot 192 = 16 + 768 = 784 = \sqrt{784} = 28.$$ $$x_1 = \frac{-4 — 28}{2} = \frac{-32}{2} = -16 \quad \text{(не подходит)}; \quad x_2 = \frac{-4 + 28}{2} = \frac{24}{2} = 12 \, \text{(км/ч)} \quad \text{— скорость первого велосипедиста}.$$

Тогда скорость второго велосипедиста:

$$x + 4 = 12 + 4 = 16 \, \text{(км/ч)}.$$

Ответ: $12 \, \text{км/ч}$ и $16 \, \text{км/ч}.$

Дано:
Пусть скорость первого велосипедиста равна $x$ км/ч, тогда скорость второго велосипедиста равна $x + 4$ км/ч. За один час первый велосипедист проедет $x$ км, а второй — $x + 4$ км. Необходимо найти скорости обоих велосипедистов, используя теорему Пифагора.

1. Составление уравнения:

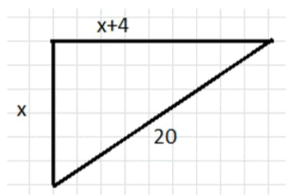
Из условия задачи известно, что первый велосипедист проезжает за 1 час $x$ км, а второй — $x + 4$ км. Если представить эти расстояния как катеты прямоугольного треугольника, то гипотенуза будет равна расстоянию между ними через час, которое равно 20 км. Применяя теорему Пифагора, получаем:

$$x^2 + (x + 4)^2 = 20^2$$

2. Раскрытие скобок:

Теперь раскроем скобки на левой стороне уравнения:

$$x^2 + (x + 4)^2 = 20^2$$ $$x^2 + (x^2 + 8x + 16) = 400$$ $$x^2 + x^2 + 8x + 16 = 400$$

3. Приведение подобных членов:

Собираем подобные члены:

$$2x^2 + 8x + 16 = 400$$

Теперь переносим 400 на левую сторону:

$$2x^2 + 8x + 16 — 400 = 0$$ $$2x^2 + 8x — 384 = 0$$

4. Упрощение уравнения:

Теперь упростим уравнение, разделив обе стороны на 2:

$$x^2 + 4x — 192 = 0$$

5. Вычисление дискриминанта:

Для решения этого квадратного уравнения вычислим дискриминант $D$ по формуле:

$$D = b^2 — 4ac$$

В уравнении $x^2 + 4x — 192 = 0$ коэффициенты $a = 1$, $b = 4$, $c = -192$. Подставляем их в формулу для дискриминанта:

$$D = 4^2 — 4 \cdot 1 \cdot (-192) = 16 + 768 = 784$$

Теперь находим корень из дискриминанта:

$$\sqrt{784} = 28$$

6. Нахождение корней уравнения:

Используем формулу для нахождения корней квадратного уравнения:

$$x = \frac{-b \pm \sqrt{D}}{2a}$$

Подставляем значения $b = 4$, $D = 784$, и $a = 1$:

$$x_1 = \frac{-4 — 28}{2} = \frac{-32}{2} = -16 \quad \text{(не подходит, так как скорость не может быть отрицательной)}$$ $$x_2 = \frac{-4 + 28}{2} = \frac{24}{2} = 12$$

7. Нахождение скорости второго велосипедиста:

Теперь, когда мы знаем скорость первого велосипедиста $x = 12$ км/ч, можем найти скорость второго велосипедиста. Он едет на 4 км/ч быстрее:

$$x + 4 = 12 + 4 = 16 \, \text{км/ч}$$

8. Ответ:

Скорость первого велосипедиста: $12 \, \text{км/ч}$.
Скорость второго велосипедиста: $16 \, \text{км/ч}$.

Ответ: $12 \, \text{км/ч}$ и $16 \, \text{км/ч}.$