ГДЗ по Алгебре 8 Класс Номер 470 Дорофеев, Суворова — Подробные Ответы

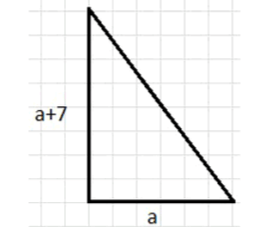
Один катет прямоугольного треугольника на 7 см больше другого, а периметр треугольника равен 30 см. Найдите все стороны треугольника.

Пусть один катет равен $a$ см. Тогда второй катет равен $a + 7$ см.
Сумма трёх сторон треугольника равна 30 см, значит гипотенуза:
$30 — a — (a + 7) = 30 — a — a — 7 = 30 — 2a — 7 = 23 — 2a$ см.
По теореме Пифагора:
$(23 — 2a)^2 = a^2 + (a + 7)^2$
Вычислим левую часть:
$(23 — 2a)^2 = 529 — 92a + 4a^2$
Вычислим правую часть:
$a^2 + (a + 7)^2 = a^2 + a^2 + 14a + 49 = 2a^2 + 14a + 49$
Составим уравнение:
$529 — 92a + 4a^2 = 2a^2 + 14a + 49$
Переносим все в одну часть:
$529 — 92a + 4a^2 — 2a^2 — 14a — 49 = 0$
Собираем подобные:
$2a^2 — 106a + 480 = 0$
Разделим на 2:
$a^2 — 53a + 240 = 0$
Вычислим дискриминант:
$D = (-53)^2 — 4 \cdot 1 \cdot 240 = 2809 — 960 = 1849$
$\sqrt{D} = 43$
Вычислим корни:
$a_1 = \frac{53 — 43}{2} = \frac{10}{2} = 5$
$a_2 = \frac{53 + 43}{2} = \frac{96}{2} = 48$ — не подходит, так как $48 > 30$
Тогда $a = 5$ см
Второй катет: $a + 7 = 5 + 7 = 12$ см
Гипотенуза: $23 — 2a = 23 — 10 = 13$ см
Ответ: $5$ см, $12$ см и $13$ см.

Пусть один из катетов прямоугольного треугольника равен $a$ см. Тогда, по условию, второй катет больше первого на 7 см и равен $a + 7$ см. Известно также, что сумма всех трёх сторон треугольника составляет 30 см. Тогда длина гипотенузы будет равна:

$30 — a — (a + 7) = 30 — a — a — 7 = 30 — 2a — 7 = 23 — 2a$ см.

Так как треугольник прямоугольный, по теореме Пифагора сумма квадратов катетов равна квадрату гипотенузы:

$a^2 + (a + 7)^2 = (23 — 2a)^2$

Вначале раскроем скобки в выражении слева:

$a^2 + (a + 7)^2 = a^2 + a^2 + 14a + 49 = 2a^2 + 14a + 49$

Теперь раскроем квадрат разности справа:

$(23 — 2a)^2 = 23^2 — 2 \cdot 23 \cdot 2a + (2a)^2 = 529 — 92a + 4a^2$

Теперь составим уравнение:

$2a^2 + 14a + 49 = 529 — 92a + 4a^2$

Перенесём все слагаемые из правой части в левую, изменяя знаки на противоположные:

$2a^2 + 14a + 49 — 529 + 92a — 4a^2 = 0$

Теперь приведём подобные слагаемые:

$(2a^2 — 4a^2) + (14a + 92a) + (49 — 529) = -2a^2 + 106a — 480 = 0$

Домножим уравнение на -1, чтобы старший коэффициент стал положительным:

$2a^2 — 106a + 480 = 0$

Разделим всё уравнение на 2:

$a^2 — 53a + 240 = 0$

Найдём дискриминант по формуле $D = b^2 — 4ac$, где $a = 1$, $b = -53$, $c = 240$:

$D = (-53)^2 — 4 \cdot 1 \cdot 240 = 2809 — 960 = 1849$

Извлекаем корень из дискриминанта:

$\sqrt{D} = \sqrt{1849} = 43$

Теперь найдём корни квадратного уравнения по формуле:

$a_1 = \frac{-(-53) — 43}{2 \cdot 1} = \frac{53 — 43}{2} = \frac{10}{2} = 5$

$a_2 = \frac{-(-53) + 43}{2 \cdot 1} = \frac{53 + 43}{2} = \frac{96}{2} = 48$

Корень $a = 48$ не удовлетворяет условию задачи, так как тогда сумма сторон была бы больше 30 см, а по условию сумма сторон равна 30 см.

Значит, подходящий корень — $a = 5$ см.

Второй катет равен:

$a + 7 = 5 + 7 = 12$ см

Гипотенуза равна:

$23 — 2a = 23 — 2 \cdot 5 = 23 — 10 = 13$ см

Ответ: $5$ см, $12$ см и $13$ см.