ГДЗ по Алгебре 8 Класс Номер 469 Дорофеев, Суворова — Подробные Ответы

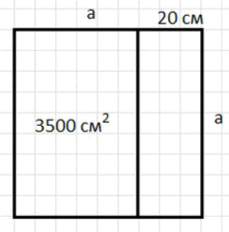
Кусок стекла имеет форму квадрата. Когда от него отрезали полосу шириной $20 \, \text{см}$, его площадь стала равна $3500 \, \text{см}^2$. Найдите первоначальные размеры куска стекла.

Пусть стороны квадратного стекла равны $a$ см, тогда после того, как от него отрезали 20 см, одна из сторон стала $a-20$ см.

Составим уравнение:

$$a(a-20)=3500$$

$$$$$$a^2-20a-3500=0$$

$$$$$$D=(-20{)}^2+4\cdot 1\cdot 3500=400+14000=14400=\sqrt{14400}=120$$

$$\mathrm{.}$$$$a_1=\frac{20-120}{2}=\frac{-100}{2}=-50\text{(не подходит)};a_2=\frac{20+120}{2}=\frac{140}{2}=70\text{(см)}\mathrm{.}$$

Ответ: первоначальные размеры куска стекла — $70\times 70\text{см}\mathrm{.}$

Дано:
Пусть сторона квадратного стекла равна $a$ см. После того как от стекла отрезали 20 см, одна из сторон стала $a-20$ см.

1. Составление уравнения:

Площадь исходного квадратного стекла равна $a^2$. После того как отрезали 20 см с одной стороны, одна сторона стала $a-20$, а площадь уменьшилась и стала равной 3500 см². Таким образом, у нас есть следующее уравнение:

$$a(a-20)=3500$$

Это уравнение описывает ситуацию, когда произведение двух сторон (исходной и уменьшенной) равно 3500 см².

2. Раскрытие скобок и преобразование уравнения:

Раскроем скобки в уравнении:

$$a(a-20)=3500$$$$a^2-20a=3500$$

Переносим все элементы на одну сторону уравнения:

$$a^2-20a-3500=0$$

Теперь у нас квадратное уравнение, которое нужно решить для $a$.

3. Вычисление дискриминанта:

Для нахождения корней квадратного уравнения используем формулу для дискриминанта $D$ для уравнения вида $a{x}^2+bx+c=0$:

$$D=b^2-4ac$$

В нашем уравнении $a=1$, $b=-20$, $c=-3500$. Подставляем эти значения в формулу для дискриминанта:

$$D=(-20{)}^2-4\cdot 1\cdot (-3500)=400+14000=14400$$

Таким образом, дискриминант $D=14400$.

4. Корень из дискриминанта:

Теперь находим корень из дискриминанта $D$:

$$\sqrt{14400}=120$$

5. Нахождение корней уравнения:

Используем формулу для нахождения корней квадратного уравнения:

$$a=\frac{-b\pm \sqrt{D}}{2a}$$

Подставляем значения $b=-20$, $D=14400$, $a=1$:

$$a_1=\frac{-(-20)-120}{2}=\frac{20-120}{2}=\frac{-100}{2}=-50$$

$$\text{(не подходит, так как сторона не может быть отрицательной)}$$

$$a_2=\frac{-(-20)+120}{2}=\frac{20+120}{2}=\frac{140}{2}=70$$

6. Ответ:

Первоначальная сторона квадратного стекла равна $70\text{см}$. Длина уменьшенной стороны после отрезания 20 см будет:

$$a-20=70-20=50\text{см}$$

Площадь после отрезания:

$$50\times 70=3500{\text{см}}^2$$

Таким образом, первоначальные размеры стекла $70\times 70\text{см}$.

Ответ: первоначальные размеры куска стекла — $70\times 70\text{см}\mathrm{.}$