ГДЗ по Алгебре 8 Класс Номер 468 Дорофеев, Суворова — Подробные Ответы
Садовый участок прямоугольной формы площадью обнесён забором, длина которого . Чему равны стороны участка? Чему равны стороны участка такой же площади, если длина забора вокруг него составляет ?
1) Пусть одна сторона равна , тогда другая сторона равна .
Составим уравнение:
2) Пусть одна сторона равна , тогда другая сторона равна .
Составим уравнение:
Ответ: и ; и .
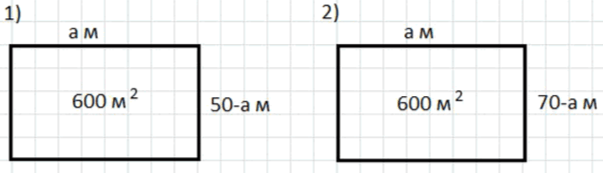
1) Пусть одна сторона равна м, тогда другая сторона равна м.
Составляем уравнение:
По условию задачи у нас есть два числа, одно из которых , а другое — , и их произведение равно 600:
Раскроем скобки:
Теперь перенесем все элементы на одну сторону:
Преобразуем уравнение:
Умножим обе стороны на , чтобы упростить решение:
Вычисление дискриминанта:
Для нахождения корней этого квадратного уравнения используем формулу для дискриминанта . В нашем уравнении , , . Подставляем эти значения:
Корень из дискриминанта:
Теперь находим корень из дискриминанта:
Нахождение корней уравнения:
Используем формулу для нахождения корней квадратного уравнения:
Подставляем значения , , :
Ответ:
Таким образом, одна сторона равна , а другая сторона равна .
Ответ: и
2) Пусть одна сторона равна м, тогда другая сторона равна м.
Составляем уравнение:
По условию задачи, произведение двух чисел и равно 600:
Раскроем скобки:
Теперь перенесем все элементы на одну сторону:
Преобразуем уравнение:
Умножим обе стороны на , чтобы упростить решение:
Вычисление дискриминанта:
Для нахождения корней этого квадратного уравнения используем формулу для дискриминанта . В нашем уравнении , , . Подставляем эти значения:
Корень из дискриминанта:
Теперь находим корень из дискриминанта:
Нахождение корней уравнения:
Используем формулу для нахождения корней квадратного уравнения:
Подставляем значения , , :
Ответ:
Таким образом, одна сторона равна , а другая сторона равна .
Ответ: и