Учебник по Алгебре для 8-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
Что выделяет этот учебник среди других:
- Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
- Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
- Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
- Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
- Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.
ГДЗ по Алгебре 8 Класс Номер 394 Дорофеев, Суворова — Подробные Ответы
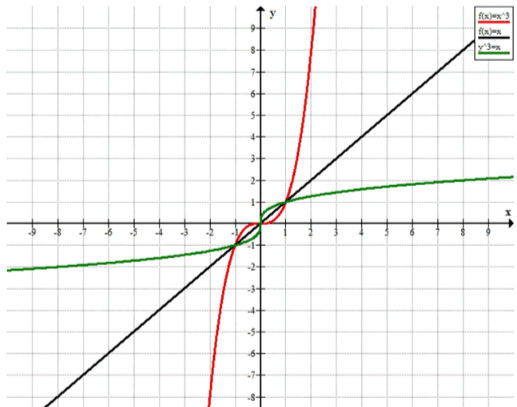
В одной системе координат постройте графики зависимостей и . Как расположены относительно прямой графики этих зависимостей?
Функции и :
У нас есть две функции:
— кубическая функция.
— кубический корень из , то есть обратная функция для .
Мы хотим доказать, что графики этих функций расположены симметрично относительно прямой .
Симметрия графиков относительно прямой :
Симметрия относительно прямой означает, что для каждой точки на графике одной функции существует точка на графике другой функции, которая симметрична ей относительно этой прямой.
Чтобы это доказать, нужно показать, что если точка лежит на графике функции , то точка лежит на графике функции , и наоборот.
Проверим симметрию:
Пусть точка лежит на графике функции . Это означает, что .
Рассмотрим точку . Чтобы эта точка лежала на графике функции , должно выполняться следующее: .
Мы знаем, что , следовательно верно, так как .
Таким образом, если точка лежит на графике функции , то точка лежит на графике функции , и наоборот.
Вывод:
Графики функций и действительно расположены симметрично относительно прямой . Это подтверждается тем, что для каждой точки на одном графике существует точка на другом графике, которая симметрична ей относительно прямой .
Таким образом, мы доказали, что графики и симметричны относительно прямой .
Алгебра