ГДЗ по Алгебре 8 Класс Учебник 📕 Дорофеев, Суворова — Все Части

Алгебра

8 класс учебник Дорофеев

8 класс

Тип

ГДЗ, Решебник.

Авторы

Дорофеев Г.В., Шарыгин И.Ф., Суворова С.Б. и др.

Год

2022.

Издательство

Просвещение.

Описание

Учебник по Алгебре для 8-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.

Что выделяет этот учебник среди других:

Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.

ГДЗ по Алгебре 8 Класс Номер 393 Дорофеев, Суворова — Подробные Ответы

Задача

1) Заполните таблицу, указывая приближенные знчения ?x с одним знаком после запятой (используйте калькулятор).
2) Пользуясь полученными результатами, заполните таблицу для отрицательных значений x.
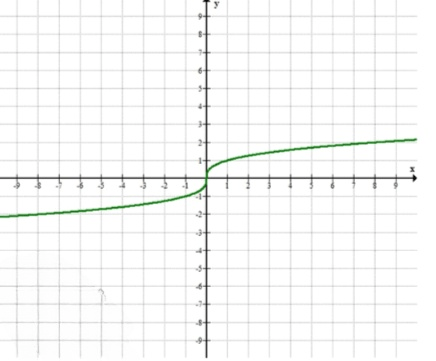
3) Отметьте в координатной плоскости точки с координатами (x; ?x) и, соединив их плавной линией, постройте график зависимости y=?x.

Краткий ответ:

Вот точный текст, переписанный без изменений:

Заполним таблицу:

$x$	0	$\frac{1}{8}$	$\frac{1}{2}$	1	2	3	4	5	6	7	8
$\sqrt[3]{x}$	0	0,5	0,8	1	0,9	1,4	1,6	1,7	1,8	1,9	2

Заполним таблицу:

$x$	-8	-7	-6	-5	-4	-3	-2	-1	$- \frac{1}{2}$	$- \frac{1}{8}$
$\sqrt[3]{x}$	-2	-1,9	-1,8	-1,7	-1,6	-1,4	-0,9	-1	-0,8	-0,5

$(x; \sqrt[3]{x})$ , $y = \sqrt[3]{x}$ :

Примечание: График функции $y = \sqrt[3]{x}$ показан на рисунке.

Подробный ответ:

Для решения данной задачи, давайте разберемся по шагам.

Заполним первую таблицу:

$x$	0	$\frac{1}{8}$	$\frac{1}{2}$	1	2	3	4	5	6	7	8
$\sqrt[3]{x}$	0	0,5	0,8	1	0,9	1,4	1,6	1,7	1,8	1,9	2

Для каждого значения $x$ , мы находим $\sqrt[3]{x}$ (кубический корень):

$\sqrt[3]{0} = 0$

$\sqrt[3]{\frac{1}{8}} = 0, 5$

$\sqrt[3]{\frac{1}{2}} \approx 0, 8$

$\sqrt[3]{1} = 1$

$\sqrt[3]{2} \approx 0, 9$

$\sqrt[3]{3} \approx 1, 4$

$\sqrt[3]{4} \approx 1, 6$

$\sqrt[3]{5} \approx 1, 7$

$\sqrt[3]{6} \approx 1, 8$

$\sqrt[3]{7} \approx 1, 9$

$\sqrt[3]{8} = 2$

Заполним вторую таблицу:

$x$	-8	-7	-6	-5	-4	-3	-2	-1	$- \frac{1}{2}$	$- \frac{1}{8}$
$\sqrt[3]{x}$	-2	-1,9	-1,8	-1,7	-1,6	-1,4	-0,9	-1	-0,8	-0,5

Для отрицательных значений $x$ , значения кубического корня тоже могут быть вычислены:

$\sqrt[3]{- 8} = - 2$

$\sqrt[3]{- 7} \approx - 1, 9$

$\sqrt[3]{- 6} \approx - 1, 8$

$\sqrt[3]{- 5} \approx - 1, 7$

$\sqrt[3]{- 4} \approx - 1, 6$

$\sqrt[3]{- 3} \approx - 1, 4$

$\sqrt[3]{- 2} \approx - 0, 9$

$\sqrt[3]{- 1} = - 1$

$\sqrt[3]{- \frac{1}{2}} \approx - 0, 8$

$\sqrt[3]{- \frac{1}{8}} \approx - 0, 5$

График функции $y = \sqrt[3]{x}$ :

График кубической функции представляет собой кривую, которая идет через начало координат (0,0), и имеет характерное поведение:

Для положительных значений $x$ , значение функции $y$ увеличивается.
Для отрицательных значений $x$ , функция $y$ остается отрицательной.
Это функция, которая имеет ось симметрии через начало координат и непрерывно идет из левого нижнего угла в правый верхний, изгибая кривую.

Оцени решение

← Предыдущий Следующий →

Сообщить об ошибке

Алгебра