ГДЗ по Алгебре 8 Класс Номер 387 Дорофеев, Суворова — Подробные Ответы
Постройте график зависимости:
а) ;
б) ;
в) ;
г) .
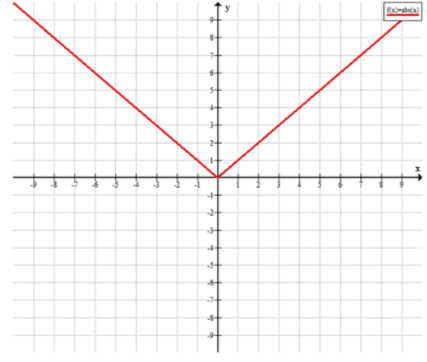
а)
Мы начинаем с выражения . Для любого , корень из квадратного значения числа всегда будет давать его абсолютную величину.
Если положительное или ноль, то , но если отрицательное, то , поэтому результат всегда равен абсолютному значению .
То есть, результатом этого выражения будет , где обозначает абсолютное значение числа .
Ответ:
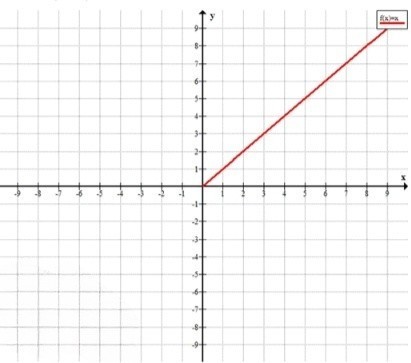
б) , при
Мы начинаем с выражения .
Квадратный корень и квадрат взаимно уничтожают друг друга. То есть , но это работает только при , потому что квадратный корень из отрицательного числа не существует в области действительных чисел.
Таким образом, для , результат будет равен .
Ответ: , при
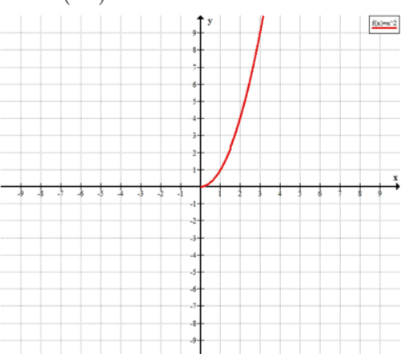
в) , при
Начинаем с выражения .
Как в предыдущем шаге, , так что выражение преобразуется в .
Мы получаем, что при , результат будет равен .
Ответ: , при
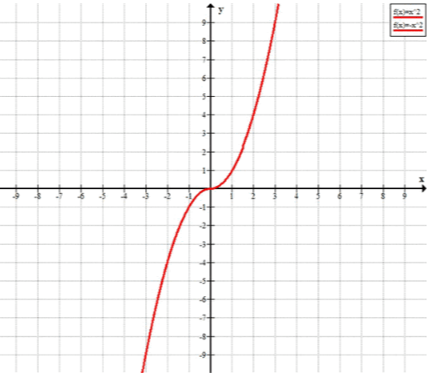
г)
Рассмотрим выражение .
Квадратный корень из равен , то есть абсолютному значению .
Таким образом, выражение становится .
Теперь анализируем результат:
- Если , то , и .
- Если , то , и .
Таким образом, результат зависит от знака . Для положительных значений получаем , а для отрицательных — .
Ответ: