ГДЗ по Алгебре 8 Класс Номер 317 Дорофеев, Суворова — Подробные Ответы

Постройте в координатной плоскости график зависимости y^2=x.

Точный текст:

$$y^2=x$$$$y=\{\begin{array}{l}\sqrt{x},\\ -\sqrt{x}\mathrm{.}\end{array}$$

Дано:

Уравнение: $y^2=x$

Перевод уравнения:

Это уравнение представляет собой стандартное квадратное уравнение относительно $y$, где $x$ является независимой переменной, а $y$ — зависимой. Решение этого уравнения можно получить, извлекая квадратный корень из обеих сторон:

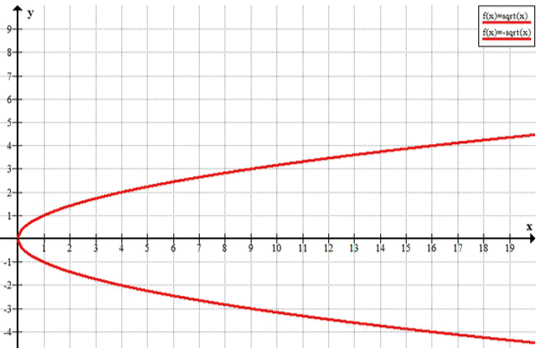
$$y=\pm \sqrt{x}$$То есть для каждого значения $x$ существуют два возможных значения $y$: одно положительное и одно отрицательное. Эти два значения $y=\sqrt{x}$ и $y=-\sqrt{x}$ будут описывать две ветви параболы, которая является графиком уравнения.

Решение уравнения:

Рассмотрим два возможных случая для $y$:

• Первый случай: $y=\sqrt{x}$
• Второй случай: $y=-\sqrt{x}$

Эти два выражения показывают, что для каждого значения $x$ (где $x\ge 0$) существуют два возможных значения для $y$: одно положительное и одно отрицательное. Это означает, что график функции будет представлять собой две симметричные ветви параболы относительно оси $x$.

Определение области определения:

Важно заметить, что для извлечения квадратного корня из $x$, $x$ должно быть неотрицательным, т.е. $x\ge 0$. Следовательно, область определения функции будет $x\ge 0$, то есть график существует только для неотрицательных значений $x$.

График функции: