ГДЗ по Алгебре 8 Класс Номер 316 Дорофеев, Суворова — Подробные Ответы

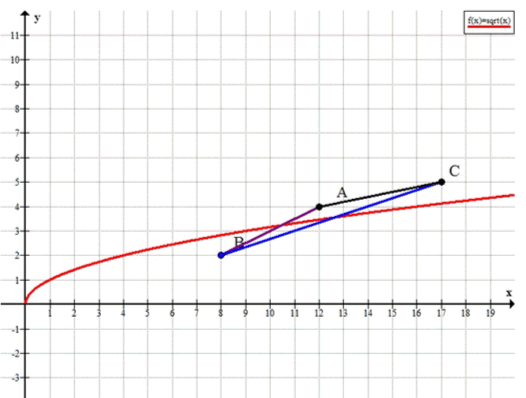
Даны точки $A(12; 4)$, $B(8; 2)$, $C(17; 5)$. Верно ли, что график функции $y = \sqrt{x}$ пересекает отрезки $AB$ и $BC$, но не пересекает отрезок $AC$?

$y=\sqrt{x}$;

$A(12;4)$; $B(8;2)$; $C(17;5)$.

Верно, что график пересекает $AB$ и $BC$;
верно, что график не пересекает $AC$.

Дано:

• Уравнение графика: $y=\sqrt{x}$
• Точки: $A(12;4)$, $B(8;2)$, $C(17;5)$

Перевод уравнения графика:

Уравнение $y=\sqrt{x}$ описывает функцию, график которой является кривой. Эта функция определена для всех $x\ge 0$, так как для отрицательных значений $x$ выражение $\sqrt{x}$ не существует в области действительных чисел. График функции будет представлять собой часть кривой, которая начинает свой путь от точки $(0,0)$ и постепенно увеличивается вправо.

Исследование пересечений с отрезками:

Для того чтобы понять, пересекает ли график функции $y=\sqrt{x}$ отрезки $AB$, $BC$ и $AC$, нужно проверить, существуют ли такие значения $x$, для которых значения функции $y=\sqrt{x}$ совпадают с $y$-координатами точек этих отрезков.

4. Проверка пересечения графика с отрезком $AB$:

Точки $A(12;4)$ и $B(8;2)$ образуют отрезок, на котором $y$-координаты изменяются от 2 до 4. Нужно проверить, существует ли такая точка на графике, для которой $y=\sqrt{x}$ принимает значение в пределах от 2 до 4.

Рассмотрим, для каких значений $x$ выполняются условия:

• $y=2\Rightarrow \sqrt{x}=2\Rightarrow x=4$
• $y=4\Rightarrow \sqrt{x}=4\Rightarrow x=16$

Таким образом, значения $y=\sqrt{x}$ на графике функции $y=\sqrt{x}$ для $x$ в интервале от 4 до 16 будут принимать значения от 2 до 4, что совпадает с интервалом значений $y$-координат точек отрезка $AB$. Следовательно, график функции пересекает отрезок $AB$.

5. Проверка пересечения графика с отрезком $BC$:

Точки $B(8;2)$ и $C(17;5)$ образуют отрезок, на котором $y$-координаты изменяются от 2 до 5. Нужно проверить, существует ли такая точка на графике, для которой $y=\sqrt{x}$ принимает значение в пределах от 2 до 5.

Рассмотрим, для каких значений $x$ выполняются условия:

• $y=2\Rightarrow \sqrt{x}=2\Rightarrow x=4$
• $y=5\Rightarrow \sqrt{x}=5\Rightarrow x=25$

Таким образом, значения $y=\sqrt{x}$ на графике функции $y=\sqrt{x}$ для $x$ в интервале от 4 до 25 будут принимать значения от 2 до 5, что совпадает с интервалом значений $y$-координат точек отрезка $BC$. Следовательно, график функции пересекает отрезок $BC$.

6. Проверка пересечения графика с отрезком $AC$:

Точки $A(12;4)$ и $C(17;5)$ образуют отрезок, на котором $y$-координаты изменяются от 4 до 5. Нужно проверить, существует ли такая точка на графике, для которой $y=\sqrt{x}$ принимает значение в пределах от 4 до 5.

Рассмотрим, для каких значений $x$ выполняются условия:

• $y=4\Rightarrow \sqrt{x}=4\Rightarrow x=16$
• $y=5\Rightarrow \sqrt{x}=5\Rightarrow x=25$

Однако, на графике функции $y=\sqrt{x}$ значения $y$ для $x$ в интервале от 16 до 25 изменяются от 4 до 5. Следовательно, для отрезка $AC$ не существует точек, где график функции пересекает этот отрезок.

7. Вывод:

• График функции $y=\sqrt{x}$ пересекает отрезки $AB$ и $BC$.
• График функции $y=\sqrt{x}$ не пересекает отрезок $AC$.

Таким образом, решение задачи подтверждает, что верно, что график функции пересекает отрезки $AB$ и $BC$, но не пересекает $AC$.