ГДЗ по Алгебре 8 Класс Учебник 📕 Дорофеев, Суворова — Все Части

Алгебра

8 класс учебник Дорофеев

8 класс

Тип

ГДЗ, Решебник.

Авторы

Дорофеев Г.В., Шарыгин И.Ф., Суворова С.Б. и др.

Год

2022.

Издательство

Просвещение.

Описание

Учебник по Алгебре для 8-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.

Что выделяет этот учебник среди других:

Понятное изложение материала. Каждая тема объясняется простым и доступным языком, что облегчает понимание даже сложных понятий.
Большое количество примеров и задач. Учебник предлагает разнообразные упражнения — от простых до более сложных, что помогает закрепить пройденный материал.
Интерактивный подход. В книге есть задания, которые побуждают учеников к самостоятельному поиску решений и развитию творческого мышления.
Связь с реальной жизнью. Многие задачи связаны с практическими ситуациями, что делает математику более живой и понятной.
Разнообразие форм подачи информации. Здесь используются таблицы, схемы, иллюстрации, что помогает лучше усваивать материал и удерживать внимание учащихся.

ГДЗ по Алгебре 8 Класс Номер 299 Дорофеев, Суворова — Подробные Ответы

Задача

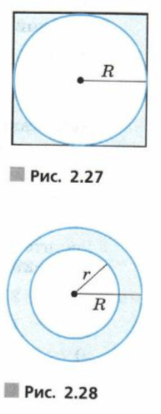
а) Составьте формулу для вычисления площади S закрашенной фигуры (рис.2.27). Выразите из этой формулы радиус круга.
б) Составьте формулу для вычисления площади S закрашенной фигуры (рис.2.28). Выразите из этой формулы радиус большого круга и радиус маленького круга.

Краткий ответ:

а) $S = (2 R)^{2} - π R^{2} = 4 R^{2} - π R^{2} = R^{2} (4 - π)$ .

$R^{2} = \frac{S}{4 - π}$

$R = \sqrt{\frac{S}{4 - π}}$ .

б) $S = π R^{2} - π r^{2} = π (R^{2} - r^{2})$ $R^{2} - r^{2} = \frac{S}{π}$
$R^{2} = \frac{S}{π} + r^{2} r^{2} = R^{2} - \frac{S}{π}$
$R = \sqrt{\frac{S}{π} + r^{2}} r = \sqrt{R^{2} - \frac{S}{π}}$ .

Подробный ответ:

а) $S = (2 R)^{2} - π R^{2} = 4 R^{2} - π R^{2} = R^{2} (4 - π)$

Начнем с уравнения для площади кольца:

$S = (2 R)^{2} - π R^{2} .$

Раскрываем квадрат в первой части:

$S = 4 R^{2} - π R^{2} .$

Выносим общий множитель $R^{2}$ за скобки:

$S = R^{2} (4 - π) .$

Для нахождения $R$ , решим это уравнение относительно $R^{2}$ :

$R^{2} = \frac{S}{4 - π} .$

Извлекаем квадратный корень из обеих частей уравнения:

$R = \sqrt{\frac{S}{4 - π}} .$

Ответ: $R = \sqrt{\frac{S}{4 - π}}$ .

б) $S = π R^{2} - π r^{2} = π (R^{2} - r^{2})$

Начнем с уравнения для площади кольца:

$S = π R^{2} - π r^{2} .$

Выносим общий множитель $π$ за скобки:

$S = π (R^{2} - r^{2}) .$

Чтобы найти $R^{2} - r^{2}$ , делим обе части уравнения на $π$ :

$R^{2} - r^{2} = \frac{S}{π} .$

Для нахождения $R^{2}$ , добавляем $r^{2}$ к обеим частям:

$R^{2} = \frac{S}{π} + r^{2} .$

Для нахождения $r^{2}$ , вычитаем $\frac{S}{π}$ из обеих частей:

$r^{2} = R^{2} - \frac{S}{π} .$

Извлекаем квадратный корень из обеих частей уравнений для $R$ и $r$ :

$R = \sqrt{\frac{S}{π} + r^{2}} и r = \sqrt{R^{2} - \frac{S}{π}} .$

Ответ: $R = \sqrt{\frac{S}{π} + r^{2}} и r = \sqrt{R^{2} - \frac{S}{π}}$ .

Оцени решение

← Предыдущий Следующий →

Сообщить об ошибке

Алгебра