ГДЗ по Алгебре 8 Класс Номер 287 Дорофеев, Суворова — Подробные Ответы

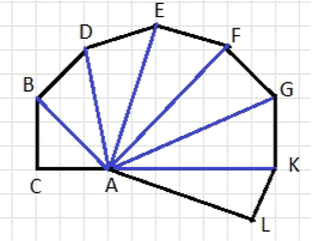
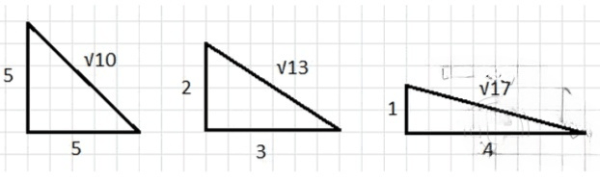
На рисунке 2.24 шесть отрезков имеют длину, равную 1.
1) Найдите длины отрезков $AB$, $AD$, $AE$, $AF$, $AG$.

2) Постройте такую же фигуру в тетради и достройте её так, чтобы получить отрезок длиной $\sqrt{8}$.

3)Отрезки длиной $\sqrt{10}$, $\sqrt{13}$, $\sqrt{17}$ можно получить, продолжив построение этой фигуры. Но для этих длин можно применить и более простой приём. Догадайтесь какой и постройте отрезки с указанными длинами.

$\mathrm{1)A}B=\sqrt{1^2+1^2}=\sqrt{1+1}=\sqrt{2}\mathrm{.}$

$AD=\sqrt{{\left(\sqrt{2}\right)}^2+1^2}=\sqrt{2+1}=\sqrt{3}\mathrm{.}$

$AE=\sqrt{{\left(\sqrt{3}\right)}^2+1^2}=\sqrt{3+1}=\sqrt{4}=2.$

$AF=\sqrt{2^2+1^2}=\sqrt{4+1}=\sqrt{5}\mathrm{.}$

$AG=\sqrt{{\left(\sqrt{5}\right)}^2+1^2}=\sqrt{5+1}=\sqrt{6}\mathrm{.}$

$\mathrm{2)A}K=\sqrt{7};AL=\sqrt{8}\mathrm{.}$

$\sqrt{10}=\sqrt{3^2+1}=\sqrt{9+1};\sqrt{10}=\sqrt{{\left(\sqrt{5}\right)}^2+{\left(\sqrt{5}\right)}^2}\mathrm{.}$

$\sqrt{13}=\sqrt{3^2+2^2}=\sqrt{9+4};\sqrt{13}=\sqrt{{\left(\sqrt{7}\right)}^2+{\left(\sqrt{6}\right)}^2}\mathrm{.}$

$\sqrt{17}=\sqrt{4^2+1^2}=\sqrt{16+1};\sqrt{17}=\sqrt{{\left(\sqrt{9}\right)}^2+{\left(\sqrt{8}\right)}^2}\mathrm{.}$

1) Вычисления длин отрезков:

а) $AB=\sqrt{1^2+1^2}$

Возводим $1$ в квадрат для каждого числа:

$$1^2=1,1^2=1.$$

Складываем их:

$$1+1=2.$$

Извлекаем квадратный корень:

$$\sqrt{2}\approx \mathrm{1.414.}$$

Таким образом, длина отрезка $AB$ равна $\sqrt{2}$.

б) $AD=\sqrt{{\left(\sqrt{2}\right)}^2+1^2}$

Возводим $\sqrt{2}$ в квадрат:

$${\left(\sqrt{2}\right)}^2=2.$$

Возводим $1$ в квадрат:

$$1^2=1.$$

Складываем:

$$2+1=3.$$

Извлекаем квадратный корень:

$$\sqrt{3}\approx \mathrm{1.732.}$$

Таким образом, длина отрезка $AD$ равна $\sqrt{3}$.

в) $AE=\sqrt{{\left(\sqrt{3}\right)}^2+1^2}$

Возводим $\sqrt{3}$ в квадрат:

$${\left(\sqrt{3}\right)}^2=3.$$

Возводим $1$ в квадрат:

$$1^2=1.$$

Складываем:

$$3+1=4.$$

Извлекаем квадратный корень:

$$\sqrt{4}=2.$$

Таким образом, длина отрезка $AE$ равна $2$.

г) $AF=\sqrt{2^2+1^2}$

Возводим $2$ в квадрат:

$$2^2=4.$$

Возводим $1$ в квадрат:

$$1^2=1.$$

Складываем:

$$4+1=5.$$

Извлекаем квадратный корень:

$$\sqrt{5}\approx \mathrm{2.236.}$$

Таким образом, длина отрезка $AF$ равна $\sqrt{5}$.

д) $AG=\sqrt{{\left(\sqrt{5}\right)}^2+1^2}$

Возводим $\sqrt{5}$ в квадрат:

$${\left(\sqrt{5}\right)}^2=5.$$

Возводим $1$ в квадрат:

$$1^2=1.$$

Складываем:

$$5+1=6.$$

Извлекаем квадратный корень:

$$\sqrt{6}\approx \mathrm{2.449.}$$

Таким образом, длина отрезка $AG$ равна $\sqrt{6}$.

2) Вычисления длин других отрезков:

а) $AK=\sqrt{7}$

Извлекаем квадратный корень из $7$:

$$\sqrt{7}\approx \mathrm{2.646.}$$

б) $AL=\sqrt{8}$

Извлекаем квадратный корень из $8$:

$$\sqrt{8}\approx \mathrm{2.828.}$$

3) Проверка равенств и вычисления:

а) $\sqrt{10}=\sqrt{3^2+1}$

Возводим $3$ в квадрат:

$$3^2=9.$$

Складываем с $1$:

$$9+1=10.$$

Извлекаем квадратный корень:

$$\sqrt{10}\approx \mathrm{3.162.}$$

б) $\sqrt{10}=\sqrt{{\left(\sqrt{5}\right)}^2+{\left(\sqrt{5}\right)}^2}$

Возводим $\sqrt{5}$ в квадрат:

$${\left(\sqrt{5}\right)}^2=5.$$

Складываем два значения:

$$5+5=10.$$

Извлекаем квадратный корень:

$$\sqrt{10}\approx \mathrm{3.162.}$$

в) $\sqrt{13}=\sqrt{3^2+2^2}$

Возводим $3$ в квадрат:

$$3^2=9.$$

Возводим $2$ в квадрат:

$$2^2=4.$$

Складываем:

$$9+4=13.$$

Извлекаем квадратный корень:

$$\sqrt{13}\approx \mathrm{3.606.}$$

г) $\sqrt{13}=\sqrt{{\left(\sqrt{7}\right)}^2+{\left(\sqrt{6}\right)}^2}$

Возводим $\sqrt{7}$ в квадрат:

$${\left(\sqrt{7}\right)}^2=7.$$

Возводим $\sqrt{6}$ в квадрат:

$${\left(\sqrt{6}\right)}^2=6.$$

Складываем:

$$7+6=13.$$

Извлекаем квадратный корень:

$$\sqrt{13}\approx \mathrm{3.606.}$$

д) $\sqrt{17}=\sqrt{4^2+1^2}$

Возводим $4$ в квадрат:

$$4^2=16.$$

Возводим $1$ в квадрат:

$$1^2=1.$$

Складываем:

$$16+1=17.$$

Извлекаем квадратный корень:

$$\sqrt{17}\approx \mathrm{4.123.}$$

е) $\sqrt{17}=\sqrt{{\left(\sqrt{9}\right)}^2+{\left(\sqrt{8}\right)}^2}$

Возводим $\sqrt{9}$ в квадрат:

$${\left(\sqrt{9}\right)}^2=9.$$

Возводим $\sqrt{8}$ в квадрат:

$${\left(\sqrt{8}\right)}^2=8.$$

Складываем:

$$9+8=17.$$

Извлекаем квадратный корень:

$$\sqrt{17}\approx \mathrm{4.123.}$$