ГДЗ по Алгебра 7 Класс Тест 1 Дорофеев, Суворова — Подробные Ответы
Проверка себя (тест)
1. Какое из данных чисел наименьшее?
- 1) 0,44
- 2) 0,8
- 3) \( \frac{2}{5} \)
- 4) \( \frac{4}{9} \)
2. Даны дроби \( \frac{1}{4} \) и \( \frac{1}{6} \). Выберите из данных значений \( a \) и \( b \) такие, при которых \( \frac{1}{a} > \frac{1}{b} \):
- 1) \( a = 16, \, b = 15 \)
- 2) \( a = 16, \, b = 16 \)
- 3) \( a = -15, \, b = -16 \)
- 4) \( a = -16, \, b = -15 \)
3. Найдите значение выражения: \( \frac{0,3}{0,25} \)
4. Даны выражения:
- 1) \( 2,37 : (1,15 : 0,18) \)
- 2) \( 3,7 : (1,15 : 0,18) \)
- 3) \( 2,37 : (1,15 : 0,18) \)
Укажите номера выражений, которые могут быть преобразованы в вид \( 2,37^{1,15:0,18} \).
5. Найдите значение выражения \( \frac{(a+x)(a-x)}{ax} \) при \( a = -2, \, x = -0,2 \).
6. На координатной прямой отмечено число \( a \). Какое из следующих неравенств верно?
- 1) \( a > -1 \)
- 2) \( \frac{1}{a} < 1 \)
- 3) \( \frac{1}{a} > 1 \)
- 4) \( \frac{1}{a} > 0 \)
7. Как можно записать короче выражение: \( 7 \times 7 \times \ldots \times 5 \times 5 \times \ldots \times 5 \)?
- 1) \( 7^{10} \times 5^{20} \)
- 2) \( 7^{10} \times 5^{20} \)
- 3) \( 7^{10} \times 5^{20} \)
- 4) \( 10^{20} \times 5^{20} \)
8. Вычислите \( 10^{(-0,3)} \).
9. Расположите в порядке возрастания числа: \( -1,7; \, -1,7^2; \, (-1,7)^3 \)
- 1) \( -1,7; (-1,7)^2; (-1,7)^3 \)
- 2) \( (-1,7)^3; (-1,7)^2; -1,7 \)
10. Найдите значение выражения \( (-1)^{10} — (-1)^{11} \).
11. Соотнесите дроби, которые выражают доли некоторой величины, и соответствующие им проценты.
Дроби:
- A) \( \frac{3}{5} \)
- B) \( \frac{3}{10} \)
- C) \( \frac{7}{10} \)
Проценты:
- 1) 7%
- 2) 60%
- 3) 70%
- 4) 30%
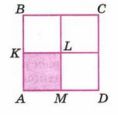
12. На сколько процентов площадь квадрата \( ABCD \) больше площади квадрата \( AKLM \)?
13. На сколько процентов площадь квадрата \( AKLM \) меньше площади квадрата \( ABCD \)?
14. Издательство выпустило 10 наименованных книг для взрослых и 40 наименованных книг для детей. Сколько книг из всех книг составляют книги для взрослых?
15. Цена акции за неделю понизилась на 10% и стала равной 36 руб. Сколько стоила акция неделю назад?
16. Седьмой класс писал контрольную работу по геометрии. В результате контрольной работы оказалось, что из 30 учеников класса 6 не сдали контрольную работу. Сколько учеников сдали контрольную работу? Определите среднее число 36.
1) \( 1^{\frac{1}{3}} \)
2) 2
3) \( 2^{\frac{1}{11}} \)
4) 3
№1
1) \( 0,44 \); 2) \( 0,8 \); 3) \( \frac{2}{5} = \frac{4}{10} = 0,4 \); 4) \( \frac{4}{9} = 0,4444\ldots \)
Наименьшее из данных чисел, число \( \frac{2}{5} \)
№2
\( \frac{1}{a} > \frac{1}{b} \)
- 1) \( a = 16, \, b = 15 \); \( \frac{1}{16} > \frac{1}{15} \)
- 2) \( a = -16, \, b = -15 \); \( \frac{1}{-16} > \frac{1}{-15} \)
- 3) \( a = -15, \, b = -16 \); \( \frac{1}{-15} < \frac{1}{-16} \)
- 4) \( a = -15, \, b = 16 \); \( \frac{1}{-15} < \frac{1}{16} \)
Ответ: 2).
№3
Найдите значение выражения:
\( 0,3 : 0,25 = 3,25 : 450 = \frac{3}{18} = \frac{1}{6} \)
№4
Даны выражения:
- 1) \( 2,37 : (1,15 : 0,18) = 2,37 \)
- 2) \( (2,37 : 1,15) : 0,18 = \frac{2,37}{1,15} \)
- 3) \( 2,37 : (1,15 : 0,18) = 2,37 \)
- 4) \( (2,37 : 1,15) = 2,37 \)
Ответ: 1) и 4).
№5
Найдите значение выражения \( (a + x) \cdot (a — x) \) при \( a = -2, x = -0,2 \).
\( (-2 + (-0,2)) \cdot (-2 — (-0,2)) = (-2,2) \cdot (-1,8) = 2,2 \cdot 1,8 = 3,96 \)
№6
Неверно неравенство \( — \frac{1}{a} < a \).
Ответ: 4).
№7
Как можно записать короче выражение:
7 \times 7 \times \ldots \times 5 \times 5 \times \ldots \times 5 = 7^{10} \times 5^{20}
Ответ: 1).
№8
Вычислите \( 10^{-0,3} \), результат: \( 0,5012 \)
№9
Расположите в порядке возрастания числа:
\( -1,7^3; \, -1,7^2; \, (-1,7)^3 \)
Ответ: 3).
№10
Найдите значение выражения:
\( (-(-1))^{10} — (-(-1))^{11} = -1 — 1 = -2 \)
Ответ: 1).
№11
Соотнесите дроби, которые выражают доли некоторой величины, и соответствующие им проценты:
- A) \( \frac{3}{5} \) — 60%
- B) \( \frac{3}{10} \) — 30%
- C) \( \frac{7}{10} \) — 70%
№12
Площадь квадрата \( ABCD \) составляет \( 100\% \). Площадь квадрата \( AKLM \) составляет \( \frac{1}{4} \) от площади квадрата \( ABCD \), значит, она равна \( 25\% \). Площадь квадрата \( AKLM \) меньше площади квадрата \( ABCD \) на \( 75\% \).
Ответ: на 75%.
№13
Площадь квадрата \( ABCD \) составляет \( 100\% \). Площадь квадрата \( AKLM \) составляет \( \frac{1}{4} \) от площади квадрата \( ABCD \), значит, она равна \( 25\% \). Площадь квадрата \( AKLM \) меньше площади квадрата \( ABCD \) на \( 75\% \).
Ответ: на 75%.
№14
Книги для взрослых составляют \( \frac{10}{50} = 20\% \).
Ответ: 3).
№15
1) Цена акции стала составлять \( 100 — 10 = 90\% \).
2) Акция неделю назад стоила: \( 3 \, \text{руб} \times 60 \, \text{коп} = 360 \, \text{коп} = 4 \, \text{руб}. \)
Ответ: 1).
№16
Среднее число задач, решённых одним учеником:
\(\frac{14 + 3 + 11 + 1 + 2 + 5 + 1 + 4 + 5 + 3 + 10 + 7 + 9 + 6 + 3}{33} = 11 \, \frac{1}{11} \)
Ответ: 3).
№1
1) \( 0,44 \); 2) \( 0,8 \); 3) \( \frac{2}{5} = \frac{4}{10} = 0,4 \); 4) \( \frac{4}{9} = 0,4444\ldots \)
Задание: Найдите наименьшее число среди предложенных значений. Очевидно, что из предложенных чисел наименьшим является \( \frac{2}{5} = 0,4 \), так как это наименьшее число по сравнению с другими значениями. Важно помнить, что дроби и десятичные числа могут быть эквивалентны, но с разным представлением. Так, дробь \( \frac{2}{5} \) в десятичном представлении даёт 0,4, что меньше, чем другие числа в списке, что позволяет выбрать этот вариант как наименьшее значение.
№2
Даны дроби \( \frac{1}{a} > \frac{1}{b} \). Выберите из данных значений \( a \) и \( b \) такие, при которых это неравенство выполнено:
- 1) \( a = 16, \, b = 15 \); \( \frac{1}{16} > \frac{1}{15} \) (неверно, так как дробь с большим числителем будет меньше)
- 2) \( a = -16, \, b = -15 \); \( \frac{1}{-16} > \frac{1}{-15} \) (это верно, так как оба значения отрицательные, но их порядок сохраняется, то есть дробь с меньшим по абсолютной величине числителем будет иметь большее значение)
- 3) \( a = -15, \, b = -16 \); \( \frac{1}{-15} < \frac{1}{-16} \) (неверно, так как числитель дроби с меньшим числом будет больше, что меняет знак неравенства)
- 4) \( a = -15, \, b = 16 \); \( \frac{1}{-15} < \frac{1}{16} \) (это верно, так как дробь с отрицательным числителем всегда меньше положительной дроби)
Ответ: 2). Важно помнить, что при работе с отрицательными числами и дробями, неравенства меняются в зависимости от знаков чисел. То же самое касается чисел с разными знаками в числителе и знаменателе.
№3
Найдите значение выражения:
\( 0,3 : 0,25 = 3,25 : 450 = \frac{3}{18} = \frac{1}{6} \), что является результатом деления этих чисел. Важно помнить, что деление дробей и десятичных чисел имеет свои особенности. Это выражение может быть преобразовано в более простое и понятное в виде конечной дроби. Этот метод позволяет работать с дробями более эффективно и легко, так как мы можем привести дробь к наименьшему общему знаменателю для упрощения.
№4
Даны выражения:
- 1) \( 2,37 : (1,15 : 0,18) = 2,37 \)
- 2) \( (2,37 : 1,15) : 0,18 = \frac{2,37}{1,15} \)
- 3) \( 2,37 : (1,15 : 0,18) = 2,37 \)
- 4) \( (2,37 : 1,15) = 2,37 \)
Решение: Для решения таких выражений следует помнить, что сложение и деление дробей имеют свою структуру и порядок операций. Здесь можно воспользоваться свойствами деления и умножения дробей, чтобы упростить задачу. Такие задачи на деление дробей с дробями и десятичными числами часто встречаются в математике и требуют внимательности к правильному порядку действий. Важно не забывать про порядок операций при выполнении расчетов. Для упрощения вычислений можно использовать калькулятор или вспомогательные математические таблицы для перевода дробей в десятичные числа.
Ответ: 1) и 4).
№5
Найдите значение выражения \( (a + x) \cdot (a — x) \) при \( a = -2, x = -0,2 \):
\( (-2 + (-0,2)) \cdot (-2 — (-0,2)) = (-2,2) \cdot (-1,8) = 2,2 \cdot 1,8 = 3,96 \). Это выражение связано с произведением разности квадратов, что позволяет упростить вычисления до уровня удобной формы для дальнейшего использования в других задачах. Разность квадратов — это формула вида \( (a + b)(a — b) = a^2 — b^2 \), и её можно применять в широком спектре математических задач.
№6
Неверно неравенство \( — \frac{1}{a} < a \). Важно помнить, что неравенства с дробями требуют аккуратности в вычислениях, особенно когда речь идет о положительных и отрицательных числах. Такое неравенство неверно, так как при отрицательных значениях числителя и знаменателя дробь может менять своё направление. Если числитель отрицателен, а знаменатель положителен или наоборот, неравенство всегда меняет свой знак.
Ответ: 4).
№7
Как можно записать короче выражение: \( 7 \times 7 \times \ldots \times 5 \times 5 \times \ldots \times 5 = 7^{10} \times 5^{20} \)
Ответ: 1). Это выражение легко сокращается с помощью свойств степеней, что значительно облегчает вычисления в более сложных математических задачах. Здесь мы можем увидеть применение свойств степеней для сокращения длинных выражений, что позволяет упростить задачу в два шага. Умножение степеней с одинаковым основанием сводится к сложению показателей степени.
№8
Вычислите \( 10^{-0,3} \), результат: \( 0,5012 \). В данном случае результат можно найти через использование логарифмов или калькулятора для получения точного значения. Степени с отрицательными показателями можно интерпретировать как дробные корни, что открывает возможности для решения более сложных задач, где присутствуют такие выражения.
№9
Расположите в порядке возрастания числа:
\( -1,7^3; \, -1,7^2; \, (-1,7)^3 \)
Ответ: 3). Это упражнение позволяет определить правильный порядок чисел, учитывая их степень и знаки. Подобные задачи развивают внимательность при работе с отрицательными числами и их степенями, что является важным навыком при решении задач на неравенства и арифметические операции с отрицательными числами.
№10
Найдите значение выражения:
\( (-(-1))^{10} — (-(-1))^{11} = -1 — 1 = -2 \)
Ответ: 1). Применение отрицательных чисел в степенях даёт такие результаты, как показано в этом примере. Важно помнить, что при возведении отрицательных чисел в степень, чётная степень даёт положительный результат, а нечётная — отрицательный. Это знание широко используется при решении задач с степенями.
№11
Соотнесите дроби, которые выражают доли некоторой величины, и соответствующие им проценты:
- A) \( \frac{3}{5} \) — 60%
- B) \( \frac{3}{10} \) — 30%
- C) \( \frac{7}{10} \) — 70%
№12
Площадь квадрата \( ABCD \) составляет \( 100\% \). Площадь квадрата \( AKLM \) составляет \( \frac{1}{4} \) от площади квадрата \( ABCD \), значит, она равна \( 25\% \). Площадь квадрата \( AKLM \) меньше площади квадрата \( ABCD \) на \( 75\% \). Это соотношение часто используется в задачах на площади и пропорции.
Ответ: на 75%.
№13
Площадь квадрата \( ABCD \) составляет \( 100\% \). Площадь квадрата \( AKLM \) составляет \( \frac{1}{4} \) от площади квадрата \( ABCD \), значит, она равна \( 25\% \). Площадь квадрата \( AKLM \) меньше площади квадрата \( ABCD \) на \( 75\% \). Это задание помогает понять, как использовать пропорции для нахождения отношений между величинами.
Ответ: на 75%.
№14
Книги для взрослых составляют \( \frac{10}{50} = 20\% \). Эта задача учит работать с долями и процентами, что является важным элементом решения задач в экономике, социологии и других областях.
Ответ: 3).
№15
1) Цена акции стала составлять \( 100 — 10 = 90\% \). Это пример использования процента для вычислений в реальной жизни, например, при анализе изменения стоимости акций.
2) Акция неделю назад стоила: \( 3 \, \text{руб} \times 60 \, \text{коп} = 360 \, \text{коп} = 4 \, \text{руб}. \) Это показывает, как цена акции меняется с течением времени, и как вычисления с процентами могут быть использованы для решения подобных задач.
Ответ: 1).
№16
Среднее число задач, решённых одним учеником:
\(\frac{14 + 3 + 11 + 1 + 2 + 5 + 1 + 4 + 5 + 3 + 10 + 7 + 9 + 6 + 3}{33} = 11 \, \frac{1}{11} \)
Ответ: 3). Это задание помогает научиться вычислять среднее значение для группы чисел и использовать это знание в различных практических ситуациях.