ГДЗ по Алгебра 7 Класс Номер 90 Дорофеев, Суворова — Подробные Ответы
Моделируем Решите задачу, используя схематические рисунки.
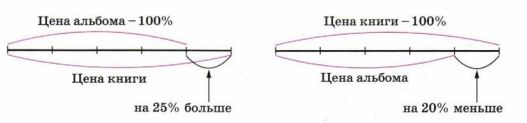
а) Книга дороже альбома на 25%. На сколько процентов альбом дешевле книги?
Решение. Цена альбома — 100%. Изобразим её каким-либо отрезком. Увеличим этот отрезок на 25%, т. е. на его длины;
получим отрезок, соответствующий цене книги (рис. 1.9).
Теперь цена книги составляет 100% (рис. 1.10). Она изображена большим отрезком. Цена альбома меньше цены книгина — этого отрезка. Так как — составляет 20%, то альбом дешевле книги на 20%.
б) Блюдце на 20% дешевле тарелки. На сколько процентов тарелка дороже блюдца?
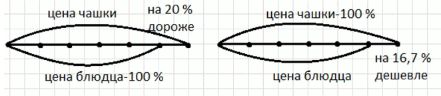
в) Чашка на 20% дороже блюдца. Какую часть стоимости чашки составляет стоимость блюдца? На сколько процентов блюдце дешевле чашки?
г) Цена книги была повышена на 10%. В конце года вновь была установлена старая цена. На сколько процентов снизили цену книги в конце года?
а) Решение в учебнике.
б) Цена тарелки = 100 %. Изобразим цену тарелки отрезком и уменьшим его на 20 %, то есть, на \( \frac{1}{5} \) его длины; полученный отрезок соответствует цене блюда.
Теперь цена блюда составляет 100 % — меньший отрезок. Цена тарелки больше цены блюда на \( \frac{1}{4} \) этого отрезка.
\( \frac{1}{4} = 25 \% \), то тарелка дороже блюда на 25 %.
в) Цена чашки = 100 %. Тогда стоимость блюда составляет \( \frac{5}{6} \) стоимости чашки, или в процентах:
\( \frac{5}{6} \cdot 100 = \frac{250}{3} = 83\frac{1}{3} \% \).
Значит, блюдце дешевле чашки на:
\( 100 — 83\frac{1}{3} = 16\frac{2}{3} \% \approx 16,7 \% \).
г) Старая цена = 100 %. Новая цена больше на 10 %. Затем примем новую цену за 100 %, тогда старая цена составляет:
\( \frac{100}{110} = \frac{10}{11} \) новой цены.
Или:
\( 100 = 1000 \div 11 = 90 \frac{10}{11} \) новой цены.
Ответ, цена снижена на \( \frac{10}{11} \) новой цены.
а) Решение в учебнике.
б) Цена тарелки = 100 %. Изобразим цену тарелки отрезком и уменьшим его на 20 %, то есть, на \( \frac{1}{5} \) его длины; полученный отрезок соответствует цене блюда.
Теперь, для того чтобы найти цену блюда, нам нужно понять, как цена блюда соотносится с ценой тарелки. После уменьшения длины отрезка на 20 %, то есть на \( \frac{1}{5} \), цена блюда составит 100 % минус меньший отрезок. То есть, из общей цены тарелки отнимаем \( \frac{1}{5} \), что дает 80 % от первоначальной цены тарелки, и эта цена соответствует цене блюда.
Далее, цена тарелки превышает цену блюда на оставшийся кусочек, равный \( \frac{1}{4} \) длины отрезка, что составляет 25 % от стоимости блюда. Таким образом, тарелка дороже блюда на 25 %.
Итак, из этого следует, что разница в цене между тарелкой и блюдом составляет 25 %, и таким образом тарелка на 25 % дороже блюда.
в) Цена чашки = 100 %. Теперь, чтобы рассчитать, сколько стоит блюдо по сравнению с чашкой, давайте примем, что стоимость блюда составляет \( \frac{5}{6} \) стоимости чашки. В процентах это выражается так:
Для того чтобы перевести дробь в проценты, умножаем её на 100:
\( \frac{5}{6} \cdot 100 = \frac{250}{3} = 83\frac{1}{3} \% \).
Это означает, что стоимость блюда составляет 83\(\frac{1}{3}\) % от стоимости чашки.
Значит, блюдце стоит меньше, чем чашка. Чтобы найти, на сколько процентов блюдце дешевле чашки, нужно вычесть 83\(\frac{1}{3}\) % из 100 %. Получаем:
\( 100 — 83\frac{1}{3} = 16\frac{2}{3} \% \).
Таким образом, блюдце дешевле чашки на 16,7 %.
г) Старая цена = 100 %. Новая цена больше на 10 %. Чтобы найти, на сколько процентов нужно снизить цену, чтобы она стала меньше на 10 %, сначала примем новую цену за 100 %, тогда старая цена составит:
Для того чтобы найти старую цену в процентах от новой, делим 100 % на 110 %, так как новая цена больше старой на 10 %:
\( \frac{100}{110} = \frac{10}{11} \) новой цены.
Или, выразив это более точно:
\( 100 = 1000 \div 11 = 90 \frac{10}{11} \) новой цены.
Таким образом, старая цена составляет 90 \(\frac{10}{11}\) % от новой цены. Это означает, что новая цена больше старой на 10 %, а сама старая цена составляет примерно 90,91 % от новой цены.
Ответ: цена снижена на \( \frac{10}{11} \) новой цены.