ГДЗ по Алгебра 7 Класс Номер 68 Дорофеев, Суворова — Подробные Ответы
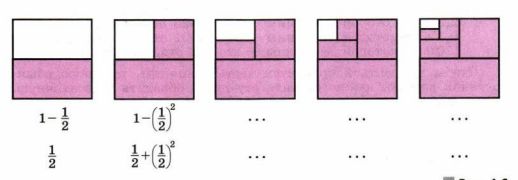
Исследуем Квадрат со стороной 1 м закрашивают по частям, как показано на рисунке 1.6. На каждом шаге закрашивается половина незакрашенной части.
1) Для первых двух квадратов записаны по два выражения для вычисления площади закрашенной части. Запишите соответствующие выражения для остальных квадратов на рисунке.
2) Запишите два разных выражения для вычисления площади закрашенной части квадрата, получившейся на десятом шаге; на сотом шаге.
3) Используйте полученный результат для вычисления значения 1/2 + (1/2)2 + (1/2)3 + …+ (1/2)10.
1) Для первого квадрата площадь закрашенной части равна 1/2:
P1 = 1/2;
2) Для второго квадрата площадь закрашенной части: 1/2 + 1/4 = 3/4:
P2 = 1/2 + 1/4 = 3/4;
3) Для третьего квадрата площадь закрашенной части: 3/4 + 1/8 = 7/8:
P3 = 3/4 + 1/8 = 7/8;
4) Для четвертого квадрата площадь закрашенной части: 7/8 + 1/16 = 15/16:
P4 = 7/8 + 1/16 = 15/16;
2) Запишите два выражения для вычисления площади закрашенной части квадрата, получившегося на десятом шаге:
P10 = 1 — (1/2)^10;
И на сотом шаге:
P100 = 1 — (1/2)^100;
3) Для вычисления суммы:
S10 = 1 — (1/2)^10 = 1023/1024;
1) Рассмотрим первый квадрат. Площадь исходного квадрата равна 1 м². На первом шаге закрашивается половина квадрата, то есть площадь закрашенной части составляет:
P1 = 1/2;
2) На втором шаге закрашивается половина оставшейся части. Если на первом шаге закрасили 1/2 квадрата, то на втором шаге будет закрашено 1/2 от оставшегося квадрата, то есть 1/4. Тогда площадь закрашенной части после второго шага будет:
P2 = 1/2 + 1/4 = 3/4;
3) На третьем шаге закрашивается половина оставшейся части, которая составляет 1/8. Таким образом, площадь закрашенной части после третьего шага равна:
P3 = 3/4 + 1/8 = 7/8;
4) На четвертом шаге закрашивается половина оставшейся части, которая составляет 1/16. Таким образом, площадь закрашенной части после четвертого шага будет:
P4 = 7/8 + 1/16 = 15/16;
2) Теперь запишем два выражения для вычисления площади закрашенной части квадрата на десятом шаге. На каждом шаге закрашивается половина оставшейся части квадрата, и площадь постепенно приближается к 1 м². Площадь закрашенной части на десятом шаге можно выразить следующим образом:
P10 = 1 — (1/2)^10;
Также площадь закрашенной части можно записать как сумму первых 10 членов геометрической прогрессии:
P10 = 1 — Σ (1/2)^n, где n от 1 до 10;
3) Для вычисления значения суммы 1/2 + (1/2)^2 + (1/2)^3 + … + (1/2)^{10}, это будет сумма первых 10 членов геометрической прогрессии с первым членом 1/2 и знаменателем 1/2. Сумма этой прогрессии будет равна:
S10 = 1 — (1/2)^10 = 1023/1024;
Таким образом, мы получили выражение для вычисления площади закрашенной части на 10-м шаге и вычислили сумму первых 10 членов прогрессии.