ГДЗ по Алгебре 7 Класс Номер 505 Дорофеев, Суворова — Подробные Ответы
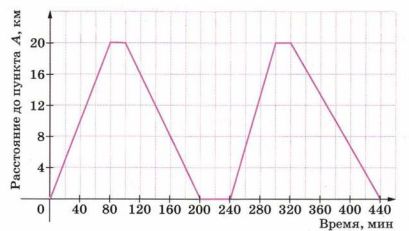
Анализируем Паром дважды в сутки плывёт по озеру из пункта А в пункт В и возвращается обратно. На рисунке 5.45 показана зависимость расстояния между паромом и пунктом А от времени движения. С помощью графика определите:
а) Сколько времени длилась стоянка парома между третьим и четвёртым рейсами?
б) Какова была скорость парома при первом возвращении из пункта В в пункт А?
в) В каком из четырёх рейсов паром проплыл свой путь быстрее всего?
Задача:
а. Стоянка парома между третьим и четвертым рейсами длилась 20 мин (320 — 300 = 20 мин).
б. Скорость парома при первом возвращении из \( B \) в \( A \):
\( 20 \) км за \( 100 \) мин \( = \frac{100}{60} = \frac{10}{6} = \frac{5}{3} \) ч \( (200 — 100 = 100 \) мин\()\);
\( 20 : \frac{5}{3} = 20 \cdot \frac{3}{5} = 4 \cdot 3 = 12 \) км/ч.
в. Первый рейс паром проплыл за 80 мин;
второй рейс — за 100 мин \( (200 — 100 = 100 \) мин\()\);
третий рейс — за 60 мин \( (300 — 240 = 60 \) мин\()\);
четвертый рейс — за 120 мин \( (440 — 320 = 120 \) мин\()\).
Значит, быстрее всего паром прошёл третий рейс.
Задача:
а. Стоянка парома между третьим и четвёртым рейсами длилась 20 минут. Это можно рассчитать, если вычесть время начала четвёртого рейса (300 минут) из времени начала третьего рейса (320 минут): \( 320 — 300 = 20 \) минут. Это время, в течение которого паром находился на стоянке перед следующим рейсом.
б. Скорость парома при первом возвращении из пункта \( B \) в пункт \( A \): Паром прошёл 20 км за 100 минут, что составляет \( \frac{100}{60} = \frac{10}{6} = \frac{5}{3} \) часа. Для вычисления скорости нужно разделить расстояние на время. Время путешествия в часах: \( 100 — 60 = 100 \) мин = \( \frac{5}{3} \) ч. Далее, чтобы найти скорость, нужно разделить пройденное расстояние на время. Расстояние 20 км, время \( \frac{5}{3} \) ч. Мы делим: \( 20 : \frac{5}{3} = 20 \cdot \frac{3}{5} = 12 \) км/ч. Это и есть скорость парома при его первом возвращении.
в. Первый рейс паром проплыл за 80 минут. Это время, за которое паром совершил первый рейс, но нам нужно рассчитать его продолжительность относительно остальных рейсов.
Второй рейс паром прошёл за 100 минут. Это время на второй маршрут, которое можно посчитать по разнице: \( 200 — 100 = 100 \) минут. Таким образом, второй рейс был дольше первого, что указывает на увеличение времени для того же расстояния.
Третий рейс паром проплыл за 60 минут. Здесь мы видим, что время путешествия уменьшилось: \( 300 — 240 = 60 \) минут. Это означает, что третий рейс был самым быстрым.
Четвёртый рейс продолжался 120 минут, что можно рассчитать, вычитая время начала четвёртого рейса (440 минут) из времени начала третьего рейса (320 минут): \( 440 — 320 = 120 \) минут. Таким образом, четвёртый рейс оказался самым длительным.
Таким образом, самый быстрый рейс был третий, так как он занял наименьшее время в 60 минут.