ГДЗ по Алгебре 7 Класс Номер 504 Дорофеев, Суворова — Подробные Ответы
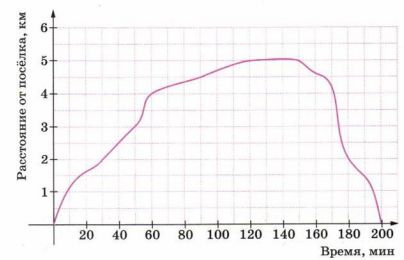
Турист поднялся из посёлка на вершину горы и затем вернулся обратно в посёлок. На рисунке 5.44 представлен график движения туриста. С помощью графика выясните:
а) Сколько времени турист пробыл на вершине горы?
б) За сколько минут турист прошёл первый километр подъёма и первый километр спуска?
в) Сколько километров турист прошёл за первые полчаса пути? за следующий час пути?
г) Через сколько времени от начала движения турист был в 2 км от посёлка?
д) Какова была средняя скорость туриста (в км/ч) на подъёме? на спуске?
а) На вершине горы турист был со 120 мин до 150 мин,
то есть, \( 150 — 120 = 30 \) мин.
б) Первый км подъема турист прошел за 9 мин, а первый км
спуска за 21 мин (171 — 150 = 21 мин).
в) За первые полчаса пути турист прошел 2 км;
за следующий час пути турист прошел: \( 4,5 \) км \( — 2 \) км \( = 2,5 \) км.
г) В 2 км от поселка турист был через 30 мин и через
180 мин \( = 3 \) ч от начала движения.
д) Турист прошел 5 км за 120 мин \( = 2 \) ч, значит, средняя
его скорость на подъеме равна \( 5 : 2 = 2,5 \) км/ч.
турист прошел 5 км за 50 мин \( = \frac{5}{6} \) ч (200 — 150 = 50 мин),
значит, средняя скорость на спуске равна \( 5 : \frac{5}{6} = 5 \cdot \frac{6}{5} = 6 \) км/ч.
a) На вершине горы турист был со 120 мин до 150 мин. Это означает, что время пребывания туриста на вершине горы составило \( 150 — 120 = 30 \) минут. То есть, он провёл на вершине горы 30 минут, что является разницей между временем, когда он пришёл и когда покинул эту точку.
б) Первый километр подъёма турист прошёл за 9 минут, что является его временем на преодоление этой дистанции при подъёме. Однако при спуске первый километр он прошёл за 21 минуту. Разница во времени между этими двумя этапами составляет \( 171 — 150 = 21 \) минута, что указывает на большую продолжительность спуска по сравнению с подъёмом.
в) За первые полчаса пути турист прошёл 2 километра. Это означает, что он двигался достаточно быстро в начале своего пути. За следующий час пути турист прошёл уже \( 4,5 \) км, но поскольку за первую половину пути было пройдено 2 км, разница составила \( 4,5 — 2 = 2,5 \) км. Это указывает на его продолжительность пути во второй части его путешествия.
г) В 2 километрах от посёлка турист был через 30 минут после начала движения, а также через 180 минут, что равно 3 часам с начала его пути. Это помогает понять, что турист уже преодолел значительное расстояние, и время, прошедшее от начала путешествия, равно 3 часам, что указывает на разницу между его текущим местоположением и начальной точкой.
д) Турист прошёл 5 км за 120 минут, что составляет 2 часа. Средняя скорость туриста на подъёме равна \( \frac{5}{2} = 2,5 \) км/ч. Это показывает, что его скорость была 2,5 километра в час при подъёме. Затем, турист прошёл 5 км за 50 минут, что эквивалентно \( \frac{5}{6} \) часа, так как \( 200 — 150 = 50 \) минут. Таким образом, его средняя скорость на спуске равна \( \frac{5}{\frac{5}{6}} = 5 \cdot \frac{6}{5} = 6 \) км/ч, что говорит о том, что спуск был гораздо быстрее, чем подъём.