ГДЗ по Алгебре 7 Класс Номер 501 Дорофеев, Суворова — Подробные Ответы

Задача

Постройте на координатной плоскости множество точек, координаты которых удовлетворяют равенству:
а) x=y2;
б) x=|y|.

Краткий ответ:

Графики уравнений

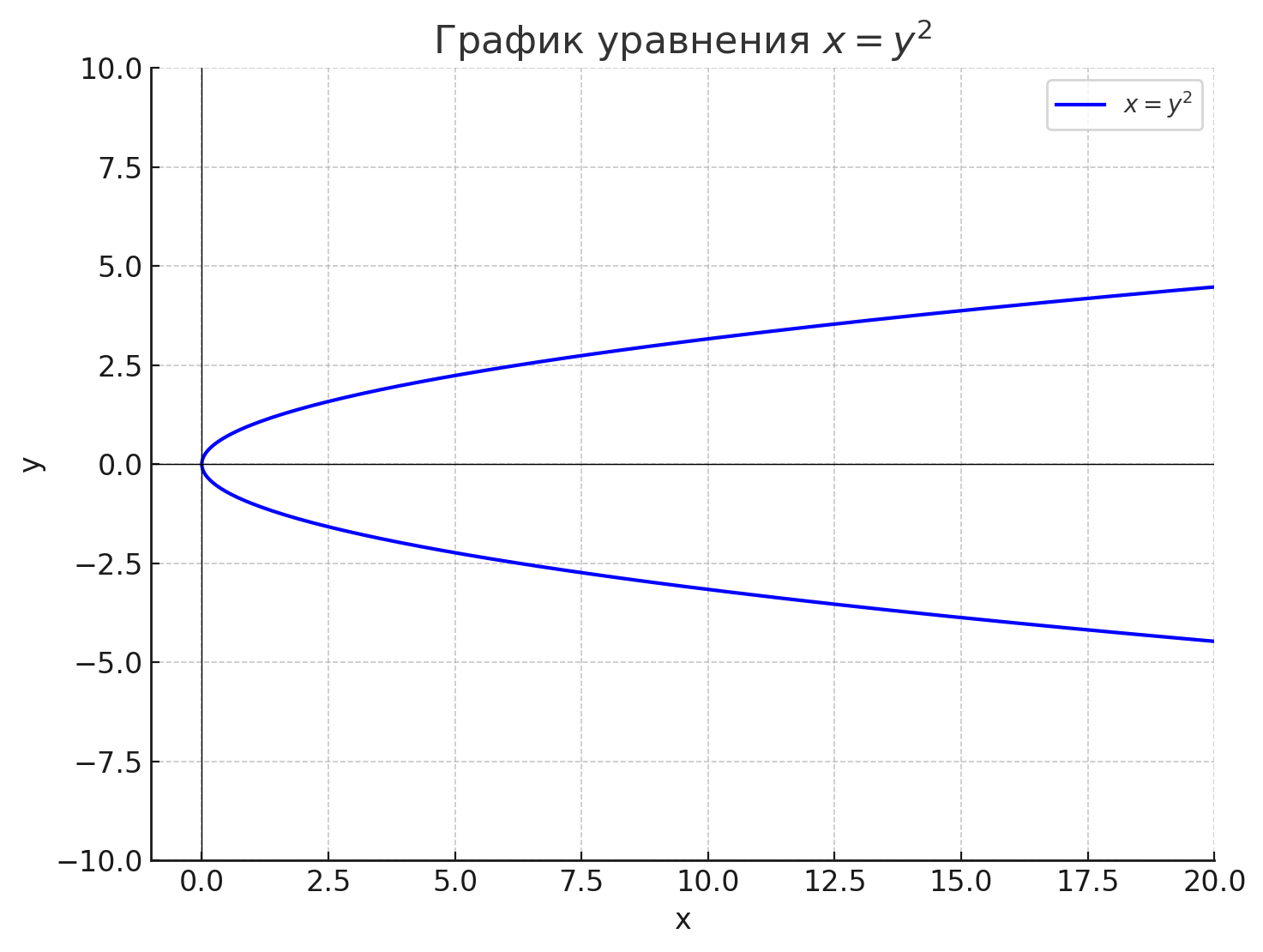
а) \( x = y^2 \)

Это уравнение описывает параболу, которая открывается вправо. В данном случае \( x \) всегда больше или равно нулю, так как \( y^2 \) всегда неотрицательно. Чтобы построить это множество точек, для разных значений \( y \) вычисляем \( x \). Например:

Когда \( y = 0 \), то \( x = 0^2 = 0 \),
Когда \( y = 1 \), то \( x = 1^2 = 1 \),
Когда \( y = -1 \), то \( x = (-1)^2 = 1 \),
Когда \( y = 2 \), то \( x = 2^2 = 4 \),
Когда \( y = -2 \), то \( x = (-2)^2 = 4 \).

Таким образом, множество точек для этого уравнения представляет собой параболу с вершиной в точке \( (0, 0) \), которая симметрична относительно оси \( x \).

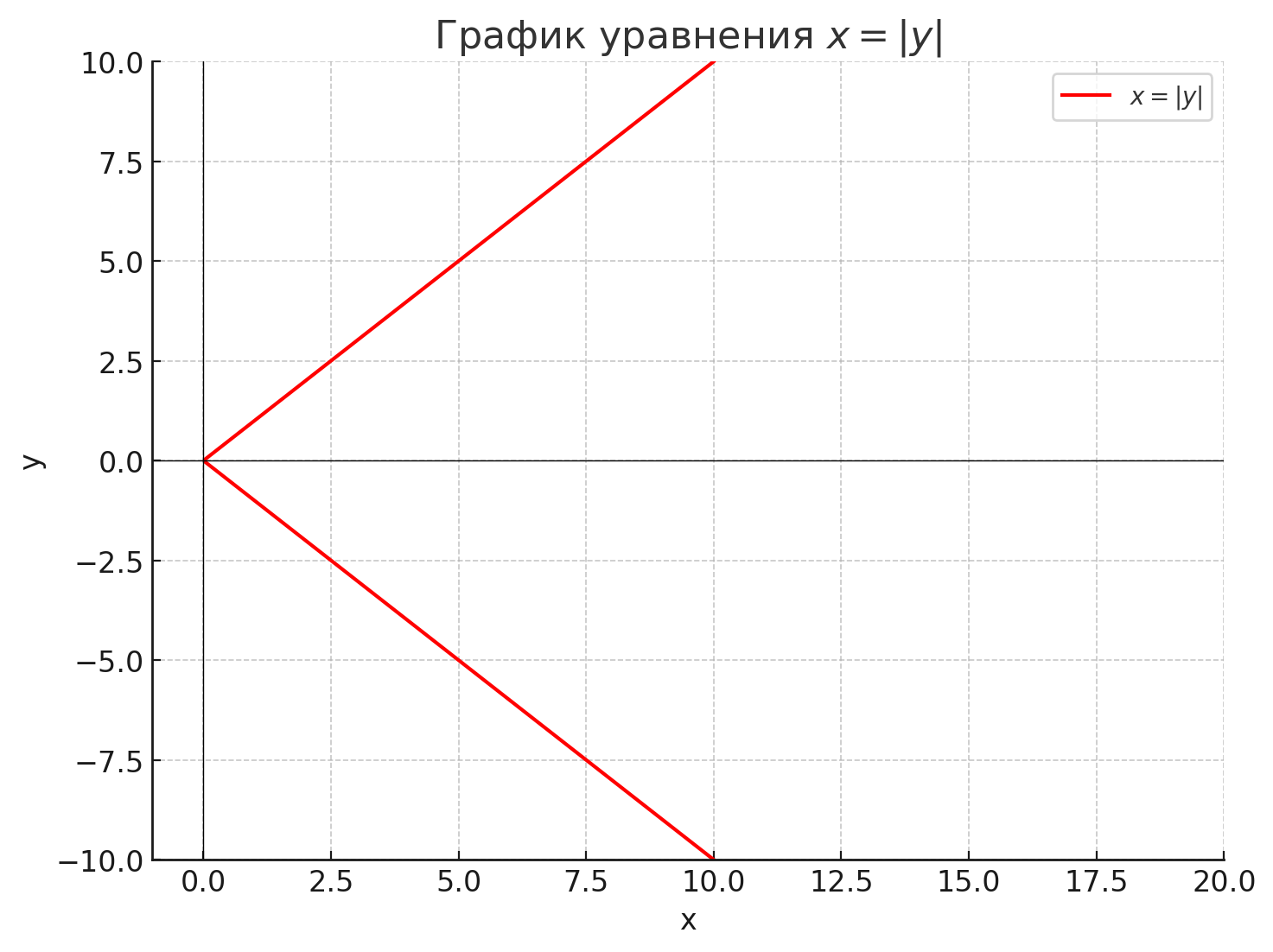
б) \( x = |y| \)

Это уравнение описывает две прямые, проходящие через начало координат. Когда \( y \) положительно или равно нулю, \( x = y \), а когда \( y \) отрицательно, \( x = -y \). В итоге, график состоит из двух прямых:

Прямая, проходящая через точки с координатами \( (x, y) = (y, y) \),
Прямая, проходящая через точки с координатами \( (x, y) = (-y, y) \).

Подробный ответ:

Это уравнение описывает параболу, которая открывается вправо. Парабола симметрична относительно оси \( x \), а её вершина находится в начале координат, то есть в точке \( (0, 0) \). При этом для любого значения переменной \( y \) значение переменной \( x \) всегда будет больше или равно нулю, так как квадрат любого числа всегда неотрицателен.

Чтобы лучше понять, как выглядит график этого уравнения, рассмотрим несколько примеров для различных значений \( y \):

Когда \( y = 0 \), то \( x = 0^2 = 0 \), график проходит через точку \( (0, 0) \),
Когда \( y = 1 \), то \( x = 1^2 = 1 \), график проходит через точку \( (1, 1) \),
Когда \( y = -1 \), то \( x = (-1)^2 = 1 \), график снова проходит через точку \( (1, -1) \),
Когда \( y = 2 \), то \( x = 2^2 = 4 \), график проходит через точку \( (4, 2) \),
Когда \( y = -2 \), то \( x = (-2)^2 = 4 \), график снова проходит через точку \( (4, -2) ).

Из этих примеров видно, что для всех положительных и отрицательных значений \( y \) значение \( x \) будет одинаковым, так как квадрат числа не зависит от его знака. Это означает, что график будет симметричен относительно оси \( x \). Внешний вид графика представляет собой классическую параболу, направленную вправо. Чем больше по модулю значение \( y \), тем больше значение \( x \), и наоборот, чем ближе \( y \) к нулю, тем меньше \( x \).

Таким образом, график этого уравнения будет иметь форму параболы с вершиной в точке \( (0, 0) \) и будет стремиться в бесконечность в сторону положительных значений \( x \), по мере увеличения \( |y| \).

Это уравнение описывает две прямые, которые пересекаются в начале координат и являются симметричными относительно оси \( y \). Прямая, проходящая через точки с положительными значениями \( y \), будет иметь уравнение \( x = y \), а прямая, проходящая через точки с отрицательными значениями \( y \), будет иметь уравнение \( x = -y \). Таким образом, график уравнения состоит из двух частей:

Первая часть — это прямая \( x = y \), которая проходит через все точки, где \( x \) и \( y \) одинаковы. Она имеет угол наклона 45 градусов к осям координат и лежит в первой и третьей четвертях координатной плоскости, где \( y \geq 0 \),
Вторая часть — это прямая \( x = -y \), которая также имеет угол наклона 45 градусов, но лежит в четвёртой и второй четвертях координатной плоскости, где \( y < 0 \).

Эти две прямые образуют угол 45 градусов с осями координат и пересекаются в начале координат \( (0, 0) \). Важно отметить, что эта фигура не является функцией в традиционном смысле, так как она не проходит тест вертикальной линии. Однако уравнение представляет собой систему, где для каждого значения \( y \) есть соответствующее значение \( x \), которое будет равно \( |y| \), то есть положительному значению \( y \).

Таким образом, график уравнения \( x = |y| \) — это две прямые, образующие угол 45 градусов с осями координат, которые идут из точки \( (0, 0) \) и продолжаются в обе стороны. Эти прямые симметричны относительно оси \( y \), и можно сказать, что их вид напоминает букву «V», стоящую на вершине.

Оцени решение