ГДЗ по Алгебре 7 Класс Номер 500 Дорофеев, Суворова — Подробные Ответы

Задача

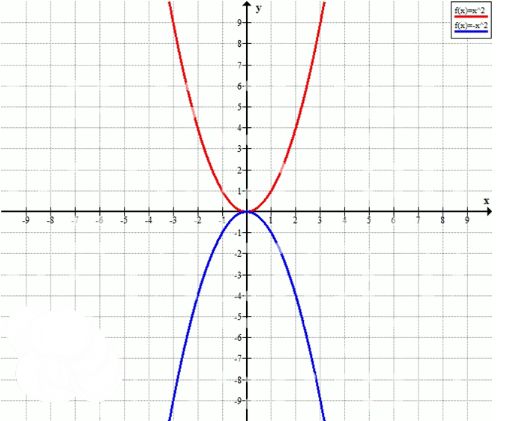
Постройте параболу, симметричную параболе у = х2 относительно оси абсцисс. Каким соотношением связаны координаты точек этой параболы?

Краткий ответ:

Функции:

\( y = x^2
\)

\( y = -x^2 \quad \text{— парабола, симметричная параболе} \, y = x^2, \text{относительно оси абсцисс.}
\)

Подробный ответ:

Функции, описывающие параболы:

1. Функция \( y = x^2 \):

Эта функция представляет собой стандартную параболу, которая открывается вверх. Вершина параболы находится в начале координат \( (0, 0) \), и она симметрична относительно оси \( y \). По мере увеличения \( |x| \), значения \( y \) увеличиваются квадратично. Эта парабола является основной функцией, которая используется в различных приложениях для моделирования роста, ускорения и многих других явлений, где есть квадратная зависимость.

2. Функция \( y = -x^2 \):

Это тоже парабола, но она открывается вниз. Вершина параболы также находится в начале координат \( (0, 0) \), но теперь ось симметрии этой параболы остаётся той же, что и для функции \( y = x^2 \). Эта парабола является зеркальным отражением параболы \( y = x^2 \) относительно оси абсцисс (оси \( x \)).

Анализ графиков:

График \( y = x^2 \): Парабола, открывающаяся вверх, с точкой минимума в \( (0, 0) \). Функция возрастает при \( x > 0 \) и убывает при \( x < 0 \).
График \( y = -x^2 \): Парабола, открывающаяся вниз, с точкой максимума в \( (0, 0) \). Функция убывает при \( x > 0 \) и возрастает при \( x < 0 \), являясь зеркальным отражением графика \( y = x^2 \) относительно оси абсцисс.

Оцени решение