ГДЗ по Алгебре 7 Класс Номер 499 Дорофеев, Суворова — Подробные Ответы
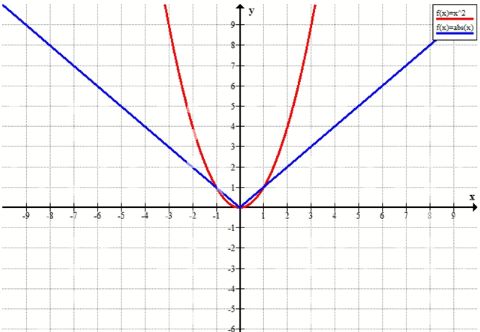
Найдите координаты общих точек графиков зависимостей у-х2 и у = |х|.
Множество точек задано функциями:
\( y = x^2 \quad \text{и} \quad y = |x|
\)
Точки пересечения графиков: \( (-1; 1) \), \( (0; 0) \), \( (1; 1) \).
Множество точек задано следующими функциями:
Для данного множества точек графики двух функций заданы следующим образом:
\( y = x^2 \quad \text{и} \quad y = |x|
\)
Анализ графиков:
Графики этих функций пересекаются в нескольких точках, которые могут быть найдены по значениям \( x \), при которых обе функции равны. Рассмотрим поведение графиков на различных интервалах значений \( x \):
- Точки пересечения: Графики функций пересекаются в трёх точках:
- Точка \( (-1; 1) \): это первая точка пересечения, где обе функции \( y = x^2 \) и \( y = |x| \) равны при \( x = -1 \), так как \( (-1)^2 = 1 \) и \( | -1 | = 1 \).
- Точка \( (0; 0) \): вторая точка пересечения, которая лежит в начале координат, где обе функции \( y = x^2 \) и \( y = |x| \) равны нулю.
- Точка \( (1; 1) \): третья точка пересечения, где при \( x = 1 \), \( y = 1^2 = 1 \) и \( |1| = 1 \).
Поведение функций на различных интервалах:
- Для \( x \geq 0 \): Обе функции \( y = x^2 \) и \( y = |x| \) совпадают и ведут себя одинаково. Для значений \( x \geq 0 \) функции принимают одинаковые значения и растут на одинаковую величину. График \( y = |x| \) представляет собой прямую линию, а график \( y = x^2 \) — параболу, которая открывается вверх.
- Для \( x < 0 \): Для отрицательных значений \( x \) график функции \( y = |x| \) будет симметричен относительно оси \( y \), а график функции \( y = x^2 \) будет параболой, которая также открывается вверх. При этом, функции начинают расходиться, так как \( |x| \) будет положительным для всех значений \( x \), в то время как \( x^2 \) остаётся всегда положительным, так как квадраты всех чисел положительны.
Заключение: Графики функций \( y = x^2 \) и \( y = |x| \) пересекаются в трёх точках: \( (-1; 1) \), \( (0; 0) \) и \( (1; 1) \). Функции имеют схожее поведение для положительных значений \( x \), но отличаются для отрицательных значений \( x \), где парабола \( y = x^2 \) остаётся выше прямой линии \( y = |x| \).