ГДЗ по Алгебре 7 Класс Номер 498 Дорофеев, Суворова — Подробные Ответы
Постройте график зависимости:
а)
\( y =
\begin{cases}
x^2, & \text{при } x > 1 \\
1, & \text{при } -1 \leq x \leq 1 \\
-x, & \text{при } x < -1
\end{cases}
\)
б)
\( y =
\begin{cases}
4, & \text{при } x \geq 2 \\
x^2, & \text{при } 0 < x < 2 \\
-x, & \text{при } x < 0
\end{cases}
\)
в)
\( y =
\begin{cases}
x, & \text{при } |x| > 1 \\
x^3, & \text{при } |x| < 1
\end{cases}
\)
а)
\( y =
\begin{cases}
x^2, & \text{при } x > 1 \\
1, & \text{при } -1 \leq x \leq 1 \\
-x, & \text{при } x < -1
\end{cases}
\)
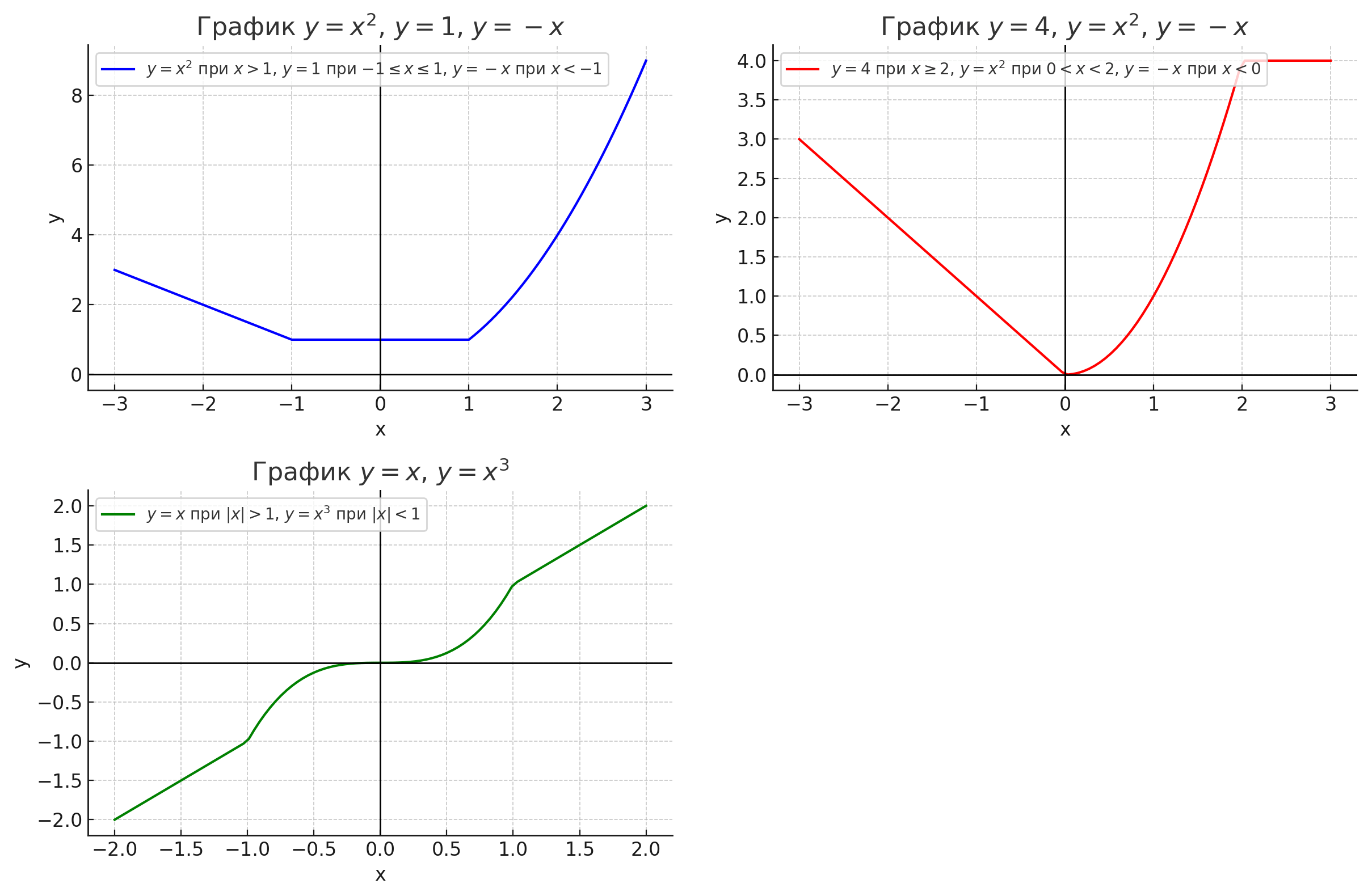
Для \( x > 1 \), функция будет параболой \( y = x^2 \).
Для \( -1 \leq x \leq 1 \), функция будет горизонтальной прямой \( y = 1 \).
Для \( x < -1 \), функция будет прямой \( y = -x \).
б)
\( y =
\begin{cases}
4, & \text{при } x \geq 2 \\
x^2, & \text{при } 0 < x < 2 \\
-x, & \text{при } x < 0
\end{cases}
\)
Для \( x \geq 2 \), функция будет горизонтальной прямой \( y = 4 \).
Для \( 0 < x < 2 \), функция будет параболой \( y = x^2 \).
Для \( x < 0 \), функция будет прямой \( y = -x \).
в)
\( y =
\begin{cases}
x, & \text{при } |x| > 1 \\
x^3, & \text{при } |x| < 1
\end{cases}
\)
Для \( |x| > 1 \), функция будет прямой \( y = x \).
Для \( |x| < 1 \), функция будет кубической кривой \( y = x^3 \).
а)
Для этого графика функция \( y \) задаётся системой, в которой её значение зависит от \( x \) и определено следующим образом:
\( y =
\begin{cases}
x^2, & \text{при } x > 1 \\
1, & \text{при } -1 \leq x \leq 1 \\
-x, & \text{при } x < -1
\end{cases}
\)
Анализ графика:
- Для \( x > 1 \): Функция будет параболой \( y = x^2 \), которая открывается вверх, начиная с точки \( (1, 1) \) и дальше, при этом значения \( y \) будут расти по мере увеличения \( x \). Для значений \( x > 1 \) график будет иметь типичную форму параболы, симметричную относительно оси \( y \).
- Для \( -1 \leq x \leq 1 \): Здесь функция будет представлять собой горизонтальную прямую \( y = 1 \), так как для всех значений \( x \) в пределах этого интервала \( y \) остаётся постоянным и равным 1.
- Для \( x < -1 \): В этой области график будет прямой линией с наклоном -1, так как функция принимает вид \( y = -x \) для всех значений \( x \) меньше -1. Линия будет проходить через начало координат с отрицательным наклоном.
б)
Этот график определяется функцией, которая меняется в зависимости от знака \( x \), и её значение задано следующим образом:
\( y =
\begin{cases}
4, & \text{при } x \geq 2 \\
x^2, & \text{при } 0 < x < 2 \\
-x, & \text{при } x < 0
\end{cases}
\)
Анализ графика:
- Для \( x \geq 2 \): Для значений \( x \geq 2 \) функция будет постоянной и равной 4, то есть график будет горизонтальной прямой, проходящей через точку \( (2, 4) \) и далее, сохраняя своё значение на уровне 4.
- Для \( 0 < x < 2 \): На этом интервале график будет параболой \( y = x^2 \), которая открывается вверх и проходит через начало координат. Парабола будет иметь минимальное значение в точке \( (0, 0) \) и возрастать до точки \( (2, 4) \).
- Для \( x < 0 \): Для отрицательных значений \( x \) график будет прямой линией с наклоном -1, так как функция \( y = -x \) будет линейной с углом наклона -1. График будет симметричен относительно оси \( y \), и значения \( y \) будут отрицательными для отрицательных значений \( x \).
в)
В этой задаче функция задается следующим образом, где \( y \) зависит от абсолютного значения \( x \):
\( y =
\begin{cases}
x, & \text{при } |x| > 1 \\
x^3, & \text{при } |x| < 1
\end{cases}
\)
Анализ графика:
- Для \( |x| > 1 \): В этой области график будет прямой линией с углом наклона 1, так как функция \( y = x \) описывает прямую, которая проходит через начало координат и имеет угол наклона 45 градусов.
- Для \( |x| < 1 \): Для значений \( |x| < 1 \), функция будет кубической кривой \( y = x^3 \), которая проходит через начало координат. Кубическая кривая будет иметь форму буквы «S», где при \( x = 0 \) значение функции будет равно 0, и она будет стремиться к нулю по обеим сторонам оси \( y \) при приближении к \( x = 0 \).