ГДЗ по Алгебре 7 Класс Номер 497 Дорофеев, Суворова — Подробные Ответы

Задача

Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют условиям:
а) y = х2 и 1 < = y < = 9;
б) у = x3 и -8 < = у < = 1;
в) у = |x| и у < = 3;
г) у — |х| и у > = 1.

Краткий ответ:

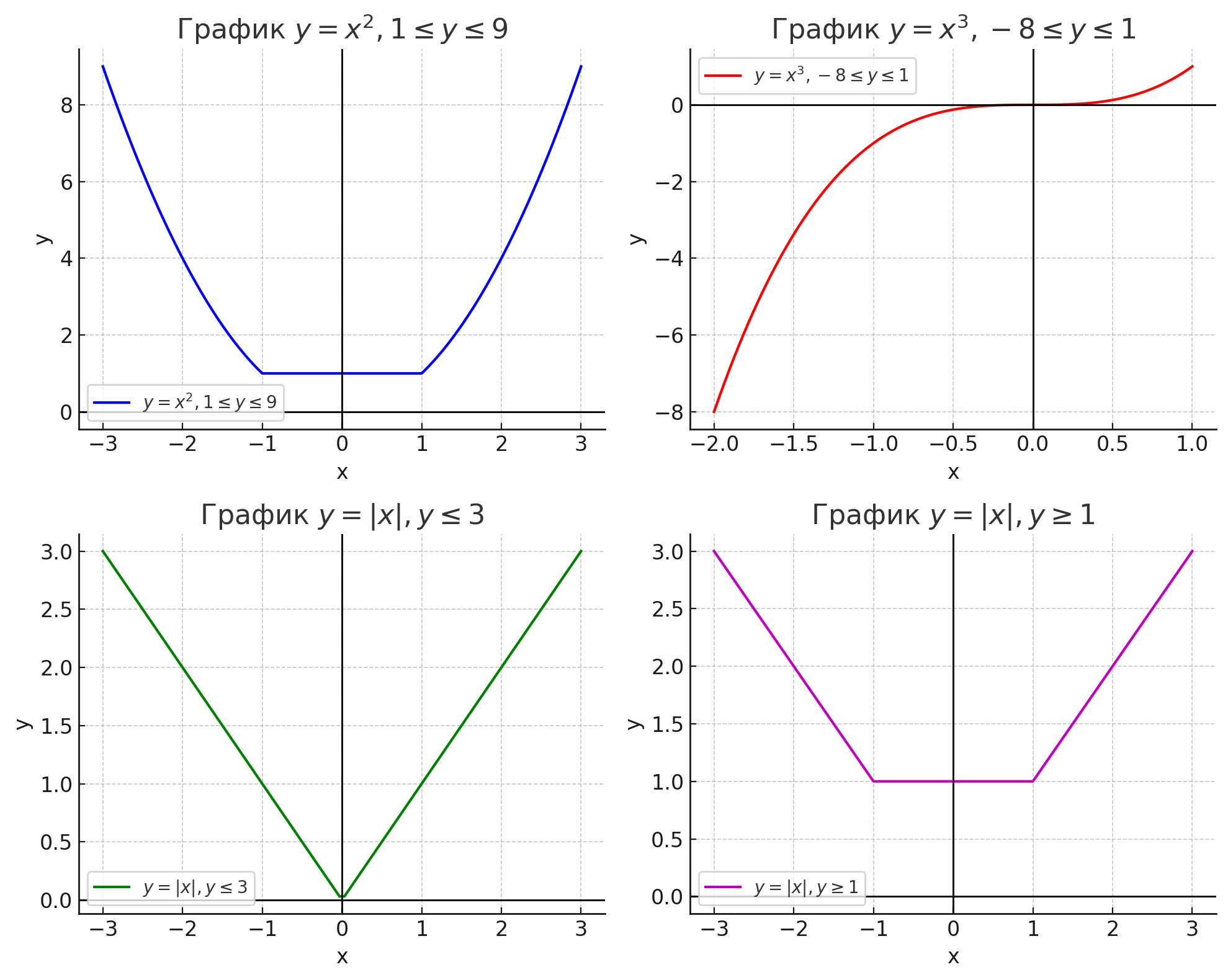
Графики для данных условий:

1. График \( y = x^2 \) и \( 1 \leq y \leq 9 \):

График функции \( y = x^2 \) ограничен значениями \( y \) от 1 до 9 для \( x \) в интервале от -3 до 3. Парабола будет расположена только в этом диапазоне значений, и все значения \( y \) будут находиться в пределах от 1 до 9.

2. График \( y = x^3 \) и \( -8 \leq y \leq 1 \):

Для функции \( y = x^3 \), график ограничен значениями \( y \) от -8 до 1, и функция будет определяться для \( x \) от -2 до 1. Кубическая кривая будет проходить через начало координат и будет ограничена по оси \( y \) на интервале от -8 до 1.

3. График \( y = |x| \) и \( y \leq 3 \):

Этот график представляет собой функцию \( y = |x| \), ограниченную значением \( y \leq 3 \). Таким образом, все значения \( y \) будут ограничены сверху значением 3 для \( x \) от -3 до 3. График будет иметь форму буквы «V», ограниченной высотой 3 по оси \( y \).

4. График \( y = |x| \) и \( y \geq 1 \):

Здесь график функции \( y = |x| \) ограничен снизу значением 1, то есть график будет начинаться от точки \( (0; 1) \) и будет продолжаться в обе стороны. Он будет представлять собой букву «V» с вершиной в \( (0; 1) \), где все значения \( y \) больше или равны 1 для всех значений \( x \).

Подробный ответ:

Графики для данных условий:

1. График \( y = x^2 \) и \( 1 \leq y \leq 9 \):

Для данного графика функция \( y = x^2 \) ограничена значениями \( y \) от 1 до 9. Это означает, что график параболы будет определяться в интервале значений \( x \), где соответствующие значения \( y \) остаются в пределах от 1 до 9. В частности:

Для \( x = -3 \), \( y = (-3)^2 = 9 \).
Для \( x = 3 \), \( y = 3^2 = 9 \).
Для \( x = 0 \), \( y = 0^2 = 0 \), но это значение выходит за пределы допустимого интервала для \( y \).
Функция будет ограничена интервалом \( x \in [-3, 3] \), так как \( x^2 = 9 \) при \( x = 3 \), и эта точка является верхней границей.

Это создаёт график параболы, ограниченный по оси \( y \) значениями от 1 до 9, а по оси \( x \) значениями от -3 до 3. Для значений \( x \) вне этого интервала функция будет выходить за пределы заданных значений для \( y \).

2. График \( y = x^3 \) и \( -8 \leq y \leq 1 \):

Этот график описывает кубическую функцию, где значения \( y \) ограничены от -8 до 1. Кубическая функция \( y = x^3 \) имеет характерную S-образную форму, и в этом случае её значения будут ограничены:

При \( x = -2 \), \( y = (-2)^3 = -8 \), что соответствует нижней границе диапазона для \( y \).
При \( x = 1 \), \( y = 1^3 = 1 \), что соответствует верхней границе диапазона для \( y \).
Функция будет проходить через начало координат, так как \( y = 0 \) при \( x = 0 \).
График будет иметь S-образную форму, при которой значения \( y \) находятся между -8 и 1, а значения \( x \) лежат в интервале от -2 до 1.

Кубическая функция будет начинаться от точки \( (-2, -8) \), проходить через начало координат \( (0, 0) \) и доходить до точки \( (1, 1) \), затем продолжать изменяться за пределами данного диапазона.

3. График \( y = |x| \) и \( y \leq 3 \):

Этот график представляет собой функцию \( y = |x| \), которая будет ограничена значением \( y = 3 \) для всех значений \( x \). Это означает, что график будет иметь форму буквы «V», где вершина находится в начале координат \( (0, 0) \), а обе её «ветви» будут направлены вверх, при этом значение \( y \) не будет превышать 3:

Для \( x = 3 \), \( y = |3| = 3 \), это верхняя граница.
Для \( x = -3 \), \( y = |-3| = 3 \), также верхняя граница.
Для всех \( x \in [-3, 3] \) значение \( y \) будет между 0 и 3.
График будет иметь форму «V», с вершиной в \( (0, 0) \) и вершины ограничены сверху значением \( y = 3 \).

4. График \( y = |x| \) и \( y \geq 1 \):

Этот график будет представлять собой ту же функцию \( y = |x| \), но с ограничением, что значения \( y \) должны быть больше или равны 1. Таким образом, график будет начинаться от точки \( (0, 1) \) и продолжаться с увеличением значения \( y \) как для положительных, так и для отрицательных значений \( x \):

Для \( x = 1 \), \( y = |1| = 1 \), точка \( (1, 1) \) — это минимальное значение для графика.
Для всех значений \( x \) больших 1 или меньших -1, значения \( y \) будут увеличиваться.
График будет «V»-образным, с вершиной в точке \( (0, 1) \), и будет идти вверх для всех значений \( x \) вне интервала \( [-1, 1] \).

Значение \( y \) будет ограничено сверху для значений \( x \) внутри интервала, а для остальных значений \( x \), график будет расти.

Оцени решение