ГДЗ по Алгебре 7 Класс Номер 496 Дорофеев, Суворова — Подробные Ответы

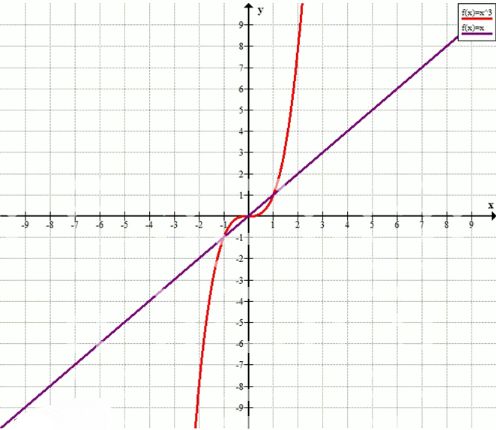
Найдите координаты точек плоскости, в которых кубическая парабола у = х3 пересекается с прямой у = х. Укажите промежутки значений х, в которых прямая расположена выше кубической параболы.

Множество точек задано функциями:

\( y = x^3 \quad \text{и} \quad y = x
\)

Точки пересечения графиков: \( (-1; -1) \), \( (0; 0) \), \( (1; 1) \).

Дополнительные замечания:

• При \( x < -1 \) и \( 0 < x < 1 \) — прямая расположена выше кубической параболы.

Множество точек задано следующими функциями:

Для данного множества точек графики двух функций определены следующим образом:

\( y = x^3 \quad \text{и} \quad y = x
\)

Точки пересечения графиков: Эти графики пересекаются в следующих точках:

• Точка \( (-1; -1) \): Первая точка пересечения графиков, где и \( y = x^3 \), и \( y = x \) совпадают, так как \( (-1)^3 = -1 \) и \( y = -1 \) для прямой \( y = x \).
• Точка \( (0; 0) \): Вторая точка пересечения, которая является общей для обеих функций, так как при \( x = 0 \), \( y = 0 \) как для кубической функции, так и для прямой.
• Точка \( (1; 1) \): Третья точка пересечения, где при \( x = 1 \), \( y = 1^3 = 1 \) и \( y = 1 \) для прямой \( y = x \).

Анализ поведения графиков на различных интервалах:

• При \( x < -1 \): Для значений \( x \) меньше -1, график функции \( y = x^3 \) будет ниже прямой \( y = x \), так как кубическая функция для таких значений \( x \) остаётся отрицательной, а прямая остаётся на положительном уровне.
• При \( 0 < x < 1 \): На этом интервале график параболы \( y = x^3 \) будет ниже прямой \( y = x \), так как при этих значениях \( x \) кубическая функция даёт меньшие значения \( y \), чем прямая.
• При \( x > 1 \): Для значений \( x \) больше 1 графики обеих функций будут совпадать, так как \( y = x^3 \) и \( y = x \) становятся равными на всем интервале \( x > 1 \).

Важные моменты:

• График функции \( y = x^3 \) представляет собой кубическую кривую, которая имеет форму S и проходит через начало координат. При \( x > 0 \) она возрастает, а при \( x < 0 \) убывает.
• График функции \( y = x \) представляет собой прямую линию с углом наклона 45 градусов, проходящую через начало координат и являющуюся диагональю квадрата.
• Пересечение этих графиков в точках \( (-1; -1) \), \( (0; 0) \) и \( (1; 1) \) означает, что эти функции равны на этих точках, но в других областях их поведение отличается.