ГДЗ по Алгебре 7 Класс Номер 495 Дорофеев, Суворова — Подробные Ответы
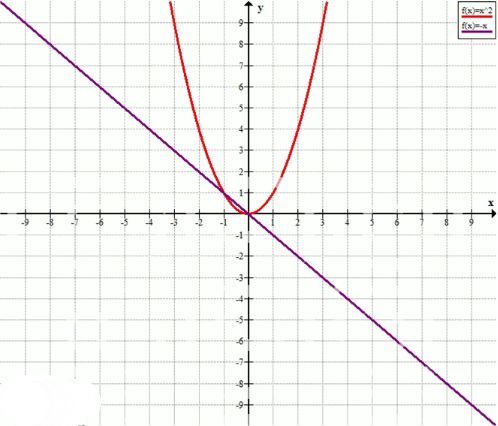
В одной системе координат постройте параболу у — х2 и прямую у = -х. Найдите координаты точек пересечения этих графиков. При каких значениях х парабола лежит выше прямой? ниже прямой?
Множество точек задано функциями:
\( y = x^2 \quad \text{и} \quad y = -x
\)
Точки пересечения графиков: \( (-1; 1) \) и \( (0; 0) \).
Дополнительные замечания:
- При \( x < -1 \) и \( x > 0 \) — парабола лежит выше прямой;
- При \( -1 < x < 0 \) — парабола лежит ниже прямой.
Множество точек задано следующими функциями:
Для данного множества точек графики двух функций определены следующим образом:
\( y = x^2 \quad \text{и} \quad y = -x
\)
Графики этих функций пересекаются в следующих точках:
- Точка \( (-1; 1) \) — первая точка пересечения графиков, которая лежит как на графике параболы \( y = x^2 \), так и на графике прямой \( y = -x \).
- Точка \( (0; 0) \) — вторая точка пересечения, которая также является общей для обеих функций.
Анализ поведения графиков на различных интервалах:
- При \( x < -1 \) и \( x > 0 \) — на этих интервалах парабола \( y = x^2 \) располагается выше прямой \( y = -x \), что означает, что значения функции \( y = x^2 \) больше, чем значения функции \( y = -x \) для этих значений \( x \).
- При \( -1 < x < 0 \) — на этом интервале график параболы \( y = x^2 \) располагается ниже графика прямой \( y = -x \), то есть значения \( y \) для параболы оказываются меньше значений \( y \) для прямой.
Важные моменты:
- График функции \( y = x^2 \) представляет собой параболу, которая открывается вверх, начиная с вершины в точке \( (0; 0) \), в то время как график функции \( y = -x \) — это прямая линия с углом наклона -1.
- Пересечение этих двух графиков в точках \( (-1; 1) \) и \( (0; 0) \) показывает, что для некоторых значений \( x \) одна функция может быть выше, а другая — ниже, в зависимости от знака \( x \).
Заключение: Графики этих двух функций показывают интересное поведение, где парабола пересекает прямую в двух точках, и в зависимости от интервала значений \( x \) одна функция может лежать выше или ниже другой.