ГДЗ по Алгебре 7 Класс Номер 494 Дорофеев, Суворова — Подробные Ответы

Постройте график зависимости, если известно, что:

а) \( y =
\begin{cases}
x^2, & \text{при } x > 0 \\
-x, & \text{при } x < 0
\end{cases}
\)

б) \( y =
\begin{cases}
-x, & \text{при } x > 0 \\
x^3, & \text{при } x < 0
\end{cases}
\)

в) \( y =
\begin{cases}
3, & \text{при } x > 3 \\
-x, & \text{при } -3 < x < 3 \\
-3, & \text{при } x \leq -3
\end{cases}
\)

г) \( y =
\begin{cases}
0, & \text{при } x > 0 \\
-x, & \text{при } -2 < x < 0 \\
2, & \text{при } x \leq -2
\end{cases}
\)

д) \( y =
\begin{cases}
|x|, & \text{при } x > 3 \\
3, & \text{при } -3 < x < 3 \\
3, & \text{при } x \leq -3
\end{cases}
\)

е) \( y =
\begin{cases}
4, & \text{при } x \leq -2 \\
x^2, & \text{при } -2 < x < 2 \\
4, & \text{при } x \geq 2
\end{cases}
\)

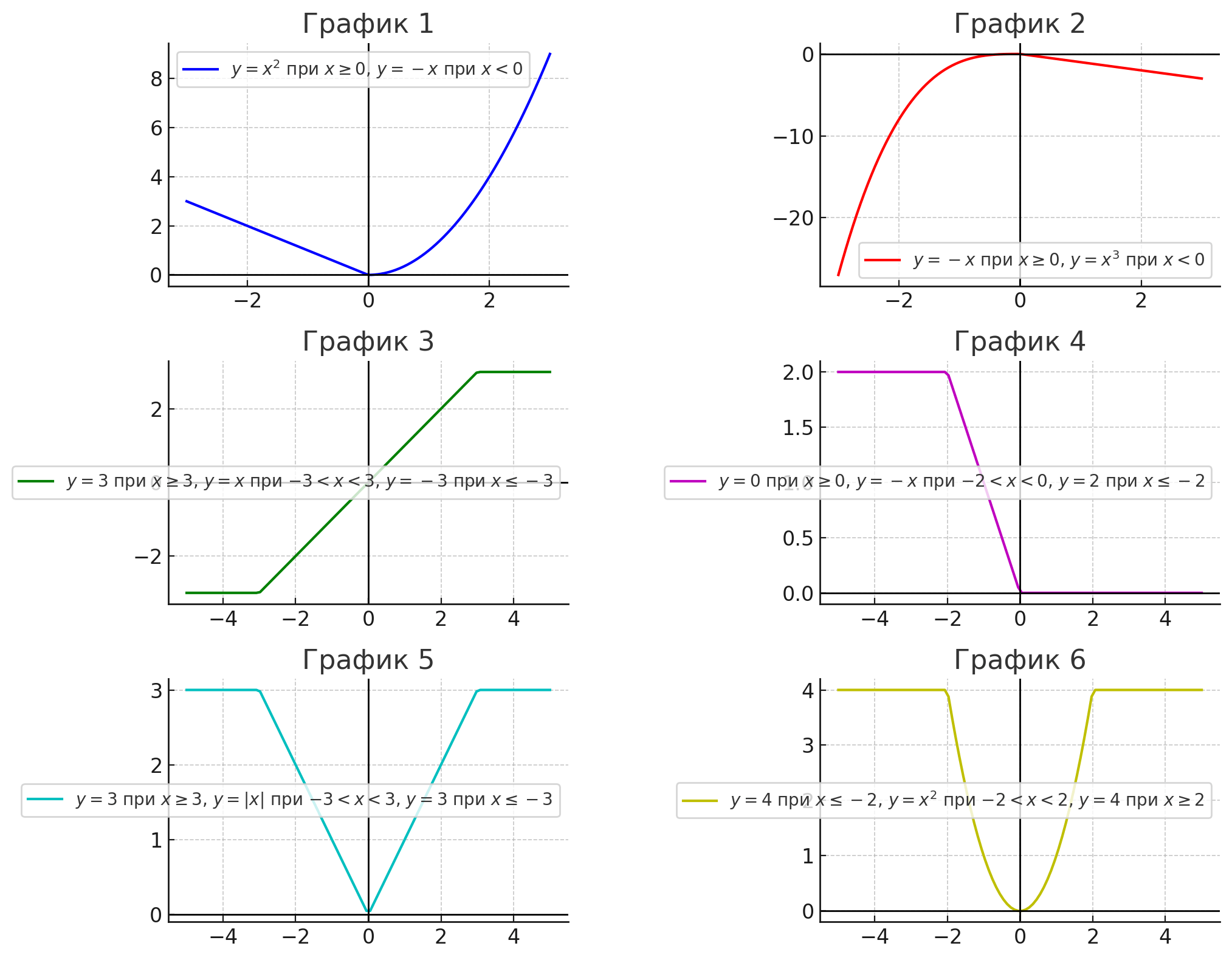
График 1:

\( y =
\begin{cases}
x^2, & \text{при } x \geq 0 \\
-x, & \text{при } x < 0
\end{cases}
\)

График 2:

\( y =
\begin{cases}
-x, & \text{при } x \geq 0 \\
x^3, & \text{при } x < 0
\end{cases}
\)

График 3:

\( y =
\begin{cases}
3, & \text{при } x \geq 3 \\
x, & \text{при } -3 < x < 3 \\
-3, & \text{при } x \leq -3
\end{cases}
\)

График 4:

\( y =
\begin{cases}
0, & \text{при } x \geq 0 \\
-x, & \text{при } -2 < x < 0 \\
2, & \text{при } x \leq -2
\end{cases}
\)

График 5:

\( y =
\begin{cases}
3, & \text{при } x \geq 3 \\
|x|, & \text{при } -3 < x < 3 \\
3, & \text{при } x \leq -3
\end{cases}
\)

График 6:

\( y =
\begin{cases}
4, & \text{при } x \leq -2 \\
x^2, & \text{при } -2 < x < 2 \\
4, & \text{при } x \geq 2
\end{cases}
\)

График 1:

Функция для этого графика определена следующим образом:

\( y =
\begin{cases}
x^2, & \text{если } x \geq 0 \\
-x, & \text{если } x < 0
\end{cases}
\)

Это означает, что для всех значений \( x \), которые больше или равны нулю, функция будет вычисляться как \( y = x^2 \), то есть график будет представлять собой параболу, направленную вверх. Для отрицательных значений \( x \), функция принимает линейное значение \( y = -x \), что будет представлять собой прямую с углом наклона -1. Этот график будет комбинированным, с параболой для положительных значений \( x \) и прямой для отрицательных значений.

График 2:

Функция для этого графика представлена следующим образом:

\( y =
\begin{cases}
-x, & \text{если } x \geq 0 \\
x^3, & \text{если } x < 0
\end{cases}
\)

Здесь для значений \( x \geq 0 \), функция \( y = -x \) будет прямой с углом наклона -1, в то время как для отрицательных значений \( x \), функция будет кубической, то есть \( y = x^3 \), и её график будет иметь характерную форму S-образной кривой. Таким образом, график состоит из прямой для положительных значений \( x \) и кубической кривой для отрицательных значений \( x \).

График 3:

Для этого графика функция задана следующими условиями:

\( y =
\begin{cases}
3, & \text{если } x \geq 3 \\
x, & \text{если } -3 < x < 3 \\
-3, & \text{если } x \leq -3
\end{cases}
\)

Этот график будет представлять собой комбинацию горизонтальных и линейных частей. Для значений \( x \geq 3 \), функция будет постоянной и равной 3, то есть горизонтальная прямая на уровне \( y = 3 \). Для значений \( -3 < x < 3 \), функция будет линейной, \( y = x \), то есть график будет представлять собой прямую линию с углом наклона 45 градусов. Для значений \( x \leq -3 \), функция снова будет постоянной и равной -3, то есть горизонтальная прямая на уровне \( y = -3 \).

График 4:

Для этого графика функция определяется так:

\( y =
\begin{cases}
0, & \text{если } x \geq 0 \\
-x, & \text{если } -2 < x < 0 \\
2, & \text{если } x \leq -2
\end{cases}
\)

График состоит из трёх частей. Для \( x \geq 0 \), \( y = 0 \), то есть это горизонтальная прямая на оси абсцисс. Для значений \( -2 < x < 0 \), график будет прямой линией с углом наклона -1. Для \( x \leq -2 \), функция будет постоянной и равной 2, то есть горизонтальная прямая на уровне \( y = 2 \).

График 5:

Для этого графика функция имеет следующую форму:

\( y =
\begin{cases}
3, & \text{если } x \geq 3 \\
|x|, & \text{если } -3 < x < 3 \\
3, & \text{если } x \leq -3
\end{cases}
\)

Этот график представляет собой две горизонтальные линии на уровнях \( y = 3 \) для \( x \geq 3 \) и \( x \leq -3 \), а также «V»-образную кривую для \( -3 < x < 3 \), представляющую собой график абсолютного значения \( y = |x| \). В области \( -3 < x < 3 \), график будет симметричным относительно оси \( y \), имея форму, подобную букве V.

График 6:

Для этого графика функция задана следующими условиями:

\( y =
\begin{cases}
4, & \text{если } x \leq -2 \\
x^2, & \text{если } -2 < x < 2 \\
4, & \text{если } x \geq 2
\end{cases}
\)

Этот график состоит из трёх частей. Для значений \( x \leq -2 \) и \( x \geq 2 \), график будет горизонтальной прямой на уровне \( y = 4 \). Для значений \( -2 < x < 2 \), график будет параболой, так как \( y = x^2 \), и эта часть графика будет представлять собой стандартную параболу, открывающуюся вверх с вершиной в начале координат.