ГДЗ по Алгебре 7 Класс Номер 493 Дорофеев, Суворова — Подробные Ответы

Задача

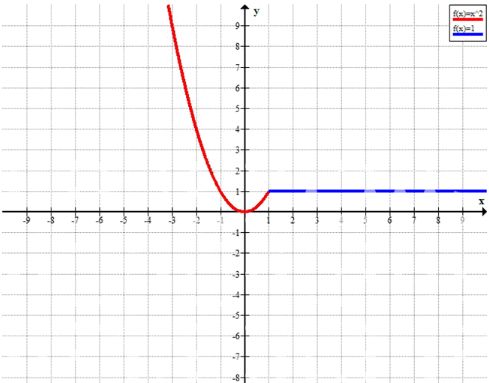
Множество точек на плоскости задано условиями:
y = система
х2 при x < = 1
1 при x > 1 .
Изобразите это множество точек на координатной плоскости.
Какие из точек (0; 0), (1/2; 1/4), (2; 4), (-2; 4), (3; 1) принадлежат этому множеству?

Краткий ответ:

Множество точек на плоскости задано функцией:

\( y =
\begin{cases}
x^2, & \text{если } x \leq 1 \\
1, & \text{если } x > 1
\end{cases}
\)

Этому множеству принадлежат точки (из данных):

(0; 0)
\( \left( \frac{1}{2}, \frac{5}{4} \right) \)
(-2; 4)
(3; 1)

Подробный ответ:

Множество точек на плоскости задано следующими условиями:

Множество точек определяется функцией, которая принимает разные значения в зависимости от знака \(x\):

\( y =
\begin{cases}
x^2, & \text{если } x \leq 1 \\
1, & \text{если } x > 1
\end{cases}
\)

Это означает, что:

Для значений \( x \leq 1 \), функция \( y = x^2 \), то есть график будет представлять собой параболу, открывающуюся вверх.
Для значений \( x > 1 \), функция \( y = 1 \), то есть для всех значений \( x \) больше единицы \( y \) будет равно 1, что представляет собой горизонтальную прямую, расположенную на уровне \( y = 1 \).

Теперь давайте рассмотрим точки, которые принадлежат этому множеству:

(0; 0): Эта точка лежит на графике функции \( y = x^2 \), так как при \( x = 0 \), \( y = 0^2 = 0 \). Следовательно, точка (0; 0) принадлежит множеству.
\( \left( \frac{1}{2}, \frac{5}{4} \right) \): При \( x = \frac{1}{2} \), значение \( y \) вычисляется как \( y = \left( \frac{1}{2} \right)^2 = \frac{1}{4} \), но точка указана с \( y = \frac{5}{4} \). Следовательно, эта точка не принадлежит множеству.
(-2; 4): При \( x = -2 \), значение \( y = (-2)^2 = 4 \), что соответствует функции \( y = x^2 \) для \( x \leq 1 \). Следовательно, точка (-2; 4) принадлежит множеству.
(3; 1): При \( x = 3 \), для \( x > 1 \), функция \( y \) принимает значение 1, так как \( y = 1 \). Следовательно, точка (3; 1) принадлежит множеству.

Итак, точки, которые принадлежат множеству, это:

(0; 0)
(-2; 4)
(3; 1)

Таким образом, данное множество точек включает в себя все точки на параболе \( y = x^2 \) для \( x \leq 1 \) и все точки на горизонтальной прямой \( y = 1 \) для \( x > 1 \). Из предложенных точек только некоторые из них удовлетворяют этим условиям.

Оцени решение