ГДЗ по Алгебре 7 Класс Номер 492 Дорофеев, Суворова — Подробные Ответы

Задача

Множество точек на плоскости задано условиями:
y = система
х при х > = 0
0 при x < 0.
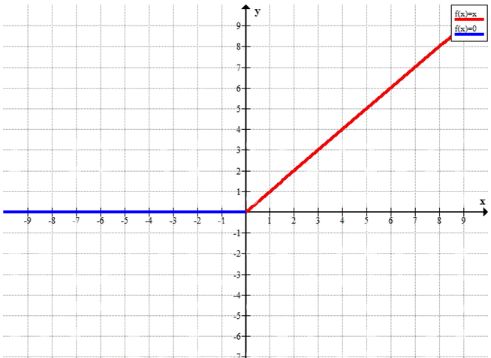
Изобразите это множество точек на координатной плоскости. Какие из точек (-1; 0), (0,6; 0,6), (1; 0), (2; 2), (-3; -3) принадлежат этому множеству?

Краткий ответ:

Множество точек на плоскости задано условиями:

\( y =
\begin{cases}
x, & x \geq 0 \\
0, & x < 0
\end{cases}
\)

Это множество точек на плоскости включает следующие точки:

(-1; 0)
(0.5; 0.5)
(2; 2)

Подробный ответ:

Множество точек на плоскости задано следующими условиями:

Множество точек определено системой, где для значений \( x \geq 0 \) функция \( y \) равна значению \( x \), а для \( x < 0 \) значение функции \( y \) равно нулю:

\( y =
\begin{cases}
x, & \text{если } x \geq 0 \\
0, & \text{если } x < 0
\end{cases}
\)

Графически это множество представляет собой две части:

Для \( x \geq 0 \), график функции \( y = x \) будет прямой линией, которая проходит через начало координат и имеет угол наклона 45 градусов.
Для \( x < 0 \), график будет горизонтальной прямой, расположенной на оси \( x \), где \( y = 0 \) для всех отрицательных значений \( x \).

Далее, рассмотрим точки, которые принадлежат этому множеству:

Точка (-1; 0): Эта точка лежит на горизонтальной прямой \( y = 0 \), которая соответствует области \( x < 0 \), где значение функции равно 0. Поэтому, точка (-1; 0) принадлежит множеству.
Точка (0.5; 0.5): Эта точка лежит на прямой \( y = x \), которая соответствует области \( x \geq 0 \). Значение \( y \) в точке 0.5 действительно равно 0.5, так как \( y = x \) для \( x \geq 0 \). Следовательно, точка (0.5; 0.5) принадлежит множеству.
Точка (2; 2): Эта точка также лежит на прямой \( y = x \) для \( x \geq 0 \), и её координаты совпадают с условием функции \( y = x \) для \( x = 2 \). Таким образом, точка (2; 2) принадлежит множеству.

Итак, все три точки, указанные выше, принадлежат множеству, так как они удовлетворяют условиям, заданным системой.

Оцени решение