ГДЗ по Алгебре 7 Класс Номер 491 Дорофеев, Суворова — Подробные Ответы
Известно, что у = х2 + 2х. Составьте таблицу соответственных значений х и у и постройте по точкам график этой зависимости. Вы получили уже знакомую вам линию. Какую?
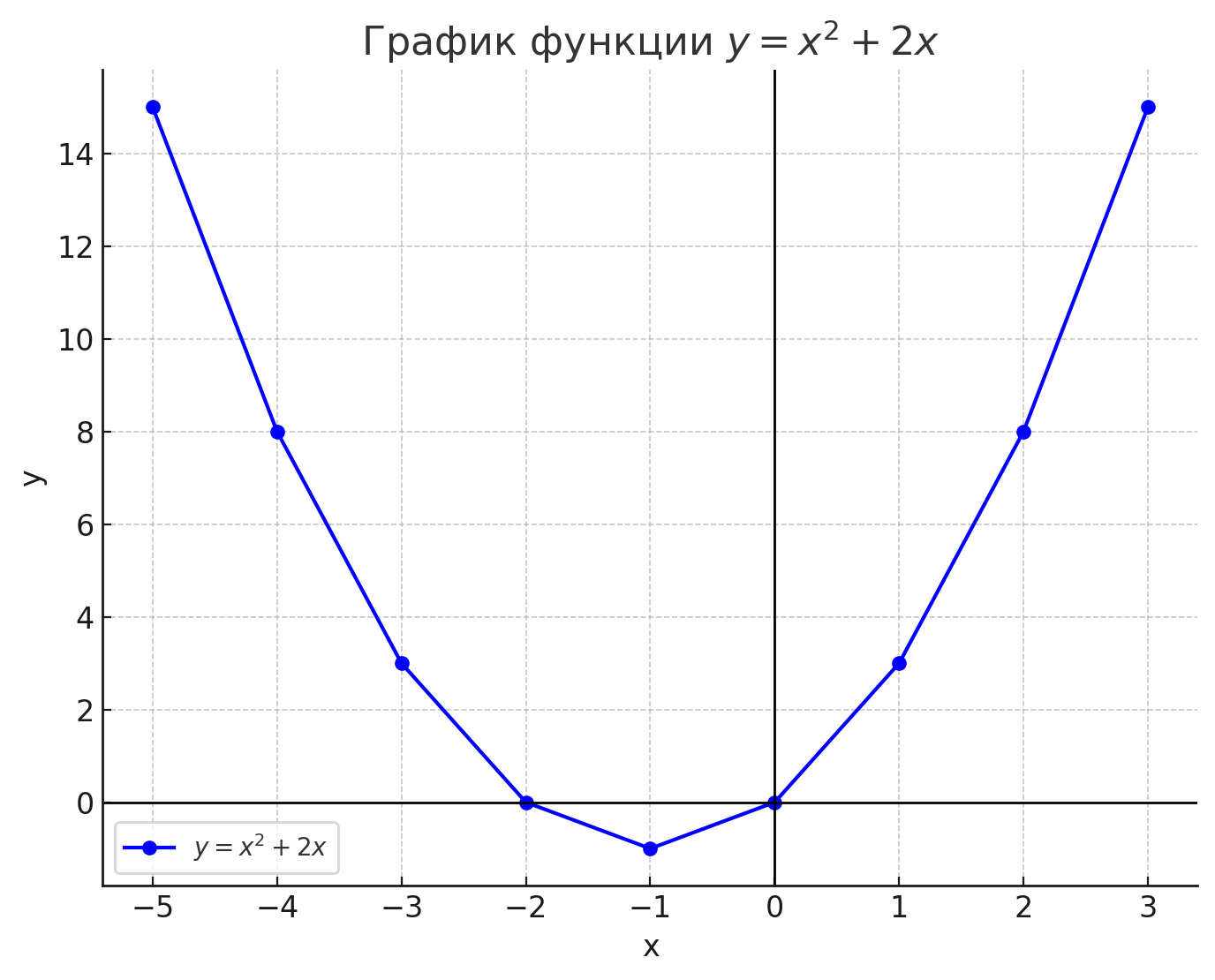
График функции \( y = x^2 + 2x \):
Для составления таблицы значений \( x \) и \( y \), а также построения графика зависимости \( y = x^2 + 2x \), мы выбрали значения \( x \) от -5 до 5 и вычислили соответствующие значения \( y \) по формуле:
| x | y = \( x^2 + 2x \) |
|---|---|
| -5 | 15 |
| -4 | 8 |
| -3 | 3 |
| -2 | 0 |
| -1 | -1 |
| 0 | 0 |
| 1 | 3 |
| 2 | 8 |
| 3 | 15 |
График этой функции представляет собой параболу, которая имеет минимум в точке \( x = -1 \) и растет в обе стороны. Он демонстрирует, как значения \( y \) изменяются в зависимости от \( x \), с четкой симметрией относительно оси \( y \).
Этот график представляет собой знакомую вам линию — параболу, которая является графиком квадратичной функции.
График функции \( y = x^2 + 2x \):
Для составления таблицы значений \( x \) и \( y \), а также построения графика зависимости \( y = x^2 + 2x \), мы выбрали несколько значений \( x \) в интервале от -5 до 5. Используя формулу \( y = x^2 + 2x \), мы вычислили соответствующие значения \( y \), что позволило построить график зависимости между этими величинами.
Таблица значений \( x \) и \( y \), полученных при подставлении различных значений \( x \) в уравнение функции \( y = x^2 + 2x \), выглядит следующим образом:
| x | y = \( x^2 + 2x \) |
|---|---|
| -5 | 15 |
| -4 | 8 |
| -3 | 3 |
| -2 | 0 |
| -1 | -1 |
| 0 | 0 |
| 1 | 3 |
| 2 | 8 |
| 3 | 15 |
График этой функции представляет собой классическую параболу, которая имеет минимум в точке \( x = -1 \) и затем растет в обе стороны, начиная с этой точки. Парабола симметрична относительно вертикальной прямой, проходящей через точку минимума (вершину), то есть оси \( x = -1 \). Важной особенностью является то, что для всех значений \( x \), кроме точки минимума, функция \( y = x^2 + 2x \) имеет положительные значения. Это также подтверждается тем, что при значениях \( x \) больше нуля, функция продолжает увеличиваться, а при отрицательных значениях \( x \) функция также растет после того, как достигнет минимума в точке \( x = -1 \).
Этот график иллюстрирует знакомую вам параболу, которая является графиком квадратичной функции. Квадратичные функции всегда описываются параболами, и её форма зависит от коэффициентов при \( x^2 \) и \( x \). В данном случае, функция имеет стандартную форму, где коэффициент при \( x^2 \) равен 1, что определяет её направление и форму. Парабола будет открываться вверх, так как коэффициент при \( x^2 \) положительный.
Таким образом, мы наблюдаем, что график функции \( y = x^2 + 2x \) является параболой, и его ключевая характеристика — минимальное значение в точке \( x = -1 \), а также симметричность относительно вертикальной оси, проходящей через эту точку.