ГДЗ по Алгебре 7 Класс Номер 490 Дорофеев, Суворова — Подробные Ответы
Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют равенству у = |х|, где:
а) х < =3; б) х > =-4; в) -2 < =x < =2.
График функции \( y = |x| \):
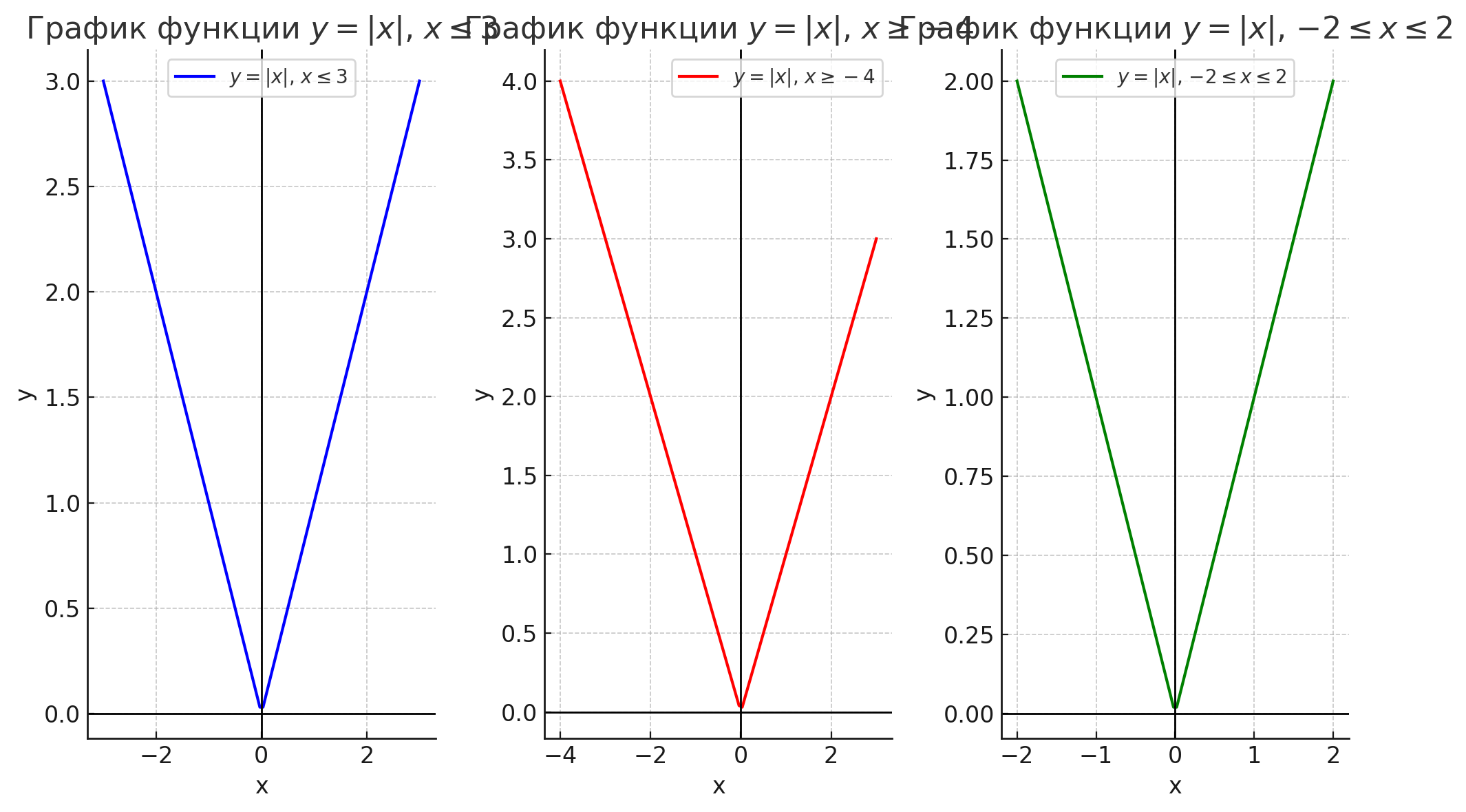
1. График функции \( y = |x| \) для интервала \( x \leq 3 \) — синим цветом:
Этот график отображает всю часть функции \( y = |x| \), где значения \( x \) варьируются от \( -\infty \) до 3. Функция будет симметричной относительно оси \( y \), и график представляет собой «V»-образную кривую, направленную вверх. Синий цвет выделяет эту часть графика, чтобы подчеркнуть изменения функции на интервале от \( -\infty \) до 3.
2. График функции \( y = |x| \) для интервала \( x \geq -4 \) — красным цветом:
График функции на интервале \( x \geq -4 \) будет охватывать значения \( x \) от -4 до \( \infty \). Здесь функция также будет симметричной относительно оси \( y \), начиная от точки \( (-4, 4) \) и продолжающейся вправо. Красный цвет выделяет этот участок графика, позволяя сконцентрироваться на положительных и отрицательных значениях \( x \), которые соответствуют растущим значениям \( y \).
3. График функции \( y = |x| \) для интервала \( -2 \leq x \leq 2 \) — зелёным цветом:
Этот график охватывает ограниченный интервал \( x \) от -2 до 2. Функция будет отображаться как «V»-образная кривая с вершиной в начале координат. Зеленый цвет выделяет эту центральную часть графика, где значения \( x \) ограничены от -2 до 2. Здесь значения функции \( y \) будут соответствовать абсолютному значению \( x \), и график будет отзеркален относительно оси \( y \).
График функции \( y = |x| \):
1. График функции \( y = |x| \) для интервала \( x \leq 3 \) — синим цветом:
График функции \( y = |x| \) на интервале \( x \leq 3 \) охватывает все значения \( x \) от \( -\infty \) до 3, и представляет собой «V»-образную кривую, которая симметрична относительно оси \( y \). Это значит, что для отрицательных значений \( x \) функция \( y \) будет принимать положительные значения, а для положительных значений \( x \) график будет повторять ту же форму, только с увеличивающимися значениями \( y \). Кривая будет направлена вверх и будет иметь точку минимума в начале координат, где \( x = 0 \). Синий цвет графика выделяет этот интервал, подчеркивая симметричность функции и её поведение на участке от \( -\infty \) до 3. Это поможет лучше визуализировать, как функция ведет себя при увеличении \( x \) и как она изменяется по мере увеличения значения \( x \) в положительную сторону.
2. График функции \( y = |x| \) для интервала \( x \geq -4 \) — красным цветом:
График функции \( y = |x| \) на интервале \( x \geq -4 \) охватывает значения \( x \) от -4 до \( \infty \). Этот участок включает в себя как отрицательные значения \( x \), так и положительные. График будет начинаться в точке \( (-4, 4) \), где \( x = -4 \) и \( y = 4 \), и будет постепенно расти, направляясь вверх и вправо, пока не будет достигать максимальных значений для больших \( x \). Для всех положительных значений \( x \) функция будет продолжать расти, увеличивая значения \( y \) на основе абсолютного значения \( x \). Красный цвет выделяет этот интервал, акцентируя внимание на том, как функция увеличивается и симметрична относительно оси \( y \), с положительными значениями \( y \) на правой части графика и отрицательными значениями на левой. Этот график помогает визуализировать поведение функции на интервале от -4 до \( \infty \), а также выявить особенности её роста и поведения для всех \( x \geq -4 \).
3. График функции \( y = |x| \) для интервала \( -2 \leq x \leq 2 \) — зелёным цветом:
График функции \( y = |x| \) на интервале \( -2 \leq x \leq 2 \) отображает ограниченную область, где \( x \) варьируется от -2 до 2. На этом интервале функция сохраняет свою форму «V», но теперь она ограничена как с отрицательной, так и с положительной стороны, что делает график симметричным относительно оси \( y \). Этот участок графика особенно полезен, если нужно анализировать поведение функции в более узком диапазоне значений \( x \). Зеленый цвет выделяет эту часть графика, подчеркивая поведение функции в области от -2 до 2. В этой области мы можем видеть, как функция возрастает от нуля в обе стороны, а её значения увеличиваются с удалением от оси \( y \). Эта часть графика также полезна для визуализации того, как абсолютное значение \( x \) влияет на рост функции и помогает наблюдать, как функция становится всё более крутой с увеличением \( x \), несмотря на то, что значения остаются положительными.
Таким образом, каждый из этих графиков представляет собой часть общей «V»-образной кривой функции \( y = |x| \), которая симметрична относительно оси \( y \). Использование разных цветов для каждого интервала позволяет выделить различные особенности функции и наглядно проиллюстрировать её поведение в пределах конкретных диапазонов значений \( x \). Эти графики помогают лучше понять, как абсолютное значение влияет на значения \( y \) для различных значений \( x \), и дают ясное представление о симметричности и росте функции на разных интервалах.