ГДЗ по Алгебре 7 Класс Номер 489 Дорофеев, Суворова — Подробные Ответы
Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют равенству у = х3, где:
а) —1 < = x < = 1;
б) х > = 0;
в) x < = 1.
График функции \( y = x^3 \):
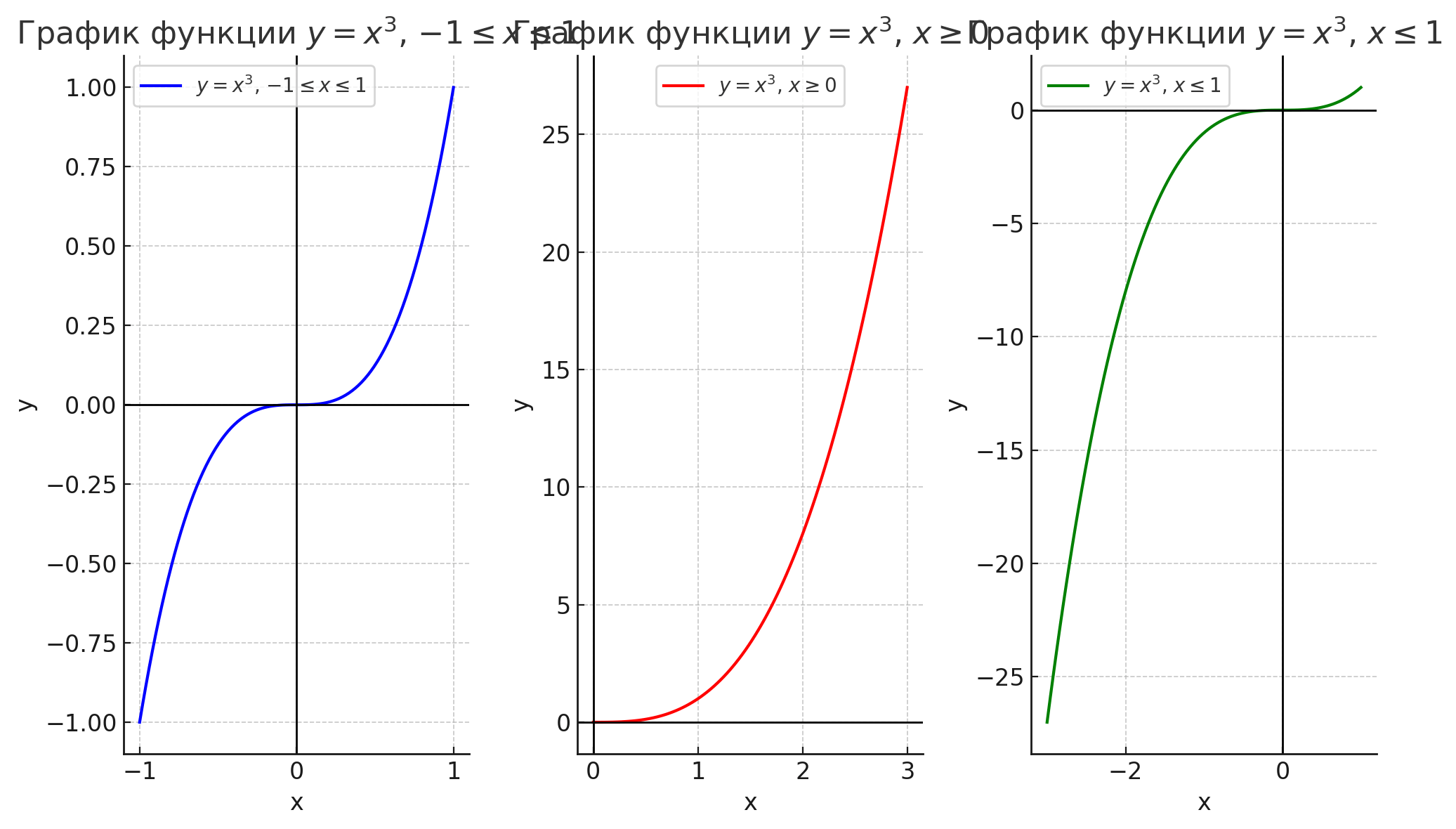
1. График функции \( y = x^3 \) для интервала \( -1 \leq x \leq 1 \) — синим цветом:
Этот график охватывает все значения \( x \) от -1 до 1, включая точку \( (0, 0) \). График представляет собой S-образную кривую, проходящую через начало координат. Синий цвет используется для выделения этого интервала на фоне других графиков.
2. График функции \( y = x^3 \) для интервала \( x \geq 0 \) — красным цветом:
Этот график отображает только правую часть кривой \( y = x^3 \), где \( x \) принимает только положительные значения и ноль. Он будет проходить через начало координат и далее будет уходить вверх, постепенно увеличивая значения \( y \). Красный цвет помогает выделить только эту часть графика.
3. График функции \( y = x^3 \) для интервала \( x \leq 1 \) — зелёным цветом:
Этот график охватывает значения \( x \) от отрицательных до 1. Это левая часть графика функции \( y = x^3 \), начиная от бесконечно малых значений \( x \) и заканчивая точкой \( (1, 1) \). Зеленый цвет выделяет эту часть графика, которая представляет собой спад функции для отрицательных значений \( x \), переходящий в рост для положительных значений.
График функции \( y = x^3 \):
1. График функции \( y = x^3 \) для интервала \( -1 \leq x \leq 1 \) — синим цветом:
Этот график охватывает все значения \( x \) от -1 до 1, включая вершину кривой в начале координат \( (0, 0) \). Функция \( y = x^3 \) является кубической функцией, и её график представляет собой S-образную кривую, которая симметрична относительно начала координат. При этом, для отрицательных значений \( x \), значение функции \( y \) будет положительным, а для положительных значений \( x \), значение \( y \) будет отрицательным. Таким образом, эта часть графика проходит через начало координат и постепенно уходит в обе стороны, имея разную кривизну на разных участках. Синий цвет выделяет эту область, что позволяет легко отслеживать изменения функции на интервале \( -1 \leq x \leq 1 \).
2. График функции \( y = x^3 \) для интервала \( x \geq 0 \) — красным цветом:
Этот график охватывает только ту часть функции, где значения \( x \) положительные или равны нулю. Это правая часть графика функции \( y = x^3 \), которая начинается в точке \( (0, 0) \), проходя через все положительные значения \( x \), где функция будет увеличиваться. Значения \( y \) на этом интервале также увеличиваются с ростом \( x \), что придает графику возрастающий характер. Этот участок графика особенно важен, поскольку на нем наблюдается непрерывный рост функции, начиная от нуля, и отсутствие изменений направления кривой. Красный цвет помогает выделить именно эту область графика и фокусировать внимание на правой части функции.
3. График функции \( y = x^3 \) для интервала \( x \leq 1 \) — зелёным цветом:
Этот график охватывает значения \( x \), которые лежат в диапазоне от отрицательных значений до 1, включая саму точку \( x = 1 \). В этой области график функции отображает левую часть параболы, где значения \( y \) для \( x < 0 \) будут отрицательными, а для \( x > 0 \) — положительными. Этот участок представляет собой спад функции на интервале от -1 до 0, который плавно переходит в рост на интервале от 0 до 1. Существует особенность, заключающаяся в том, что при отрицательных значениях \( x \), функция убывает, а при положительных значениях начинает расти. Зеленый цвет выделяет эту часть графика, что позволяет акцентировать внимание на левом участке функции, где значение функции меняет знак.
Каждый из этих графиков представляет собой лишь часть полной S-образной кривой функции \( y = x^3 \), но с выделением определенных интервалов. С помощью различного цветового выделения можно четко наблюдать как поведение функции меняется в зависимости от значений \( x \). Эти графики позволяют более глубоко проанализировать поведение кубической функции на различных участках координатной плоскости.