ГДЗ по Алгебре 7 Класс Номер 488 Дорофеев, Суворова — Подробные Ответы
Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют равенству у = х2, где:
а) -3 < = х < = 3;
б) -2 < = x < = 1;
в) х < =0.
График функции \( y = x^2 \):
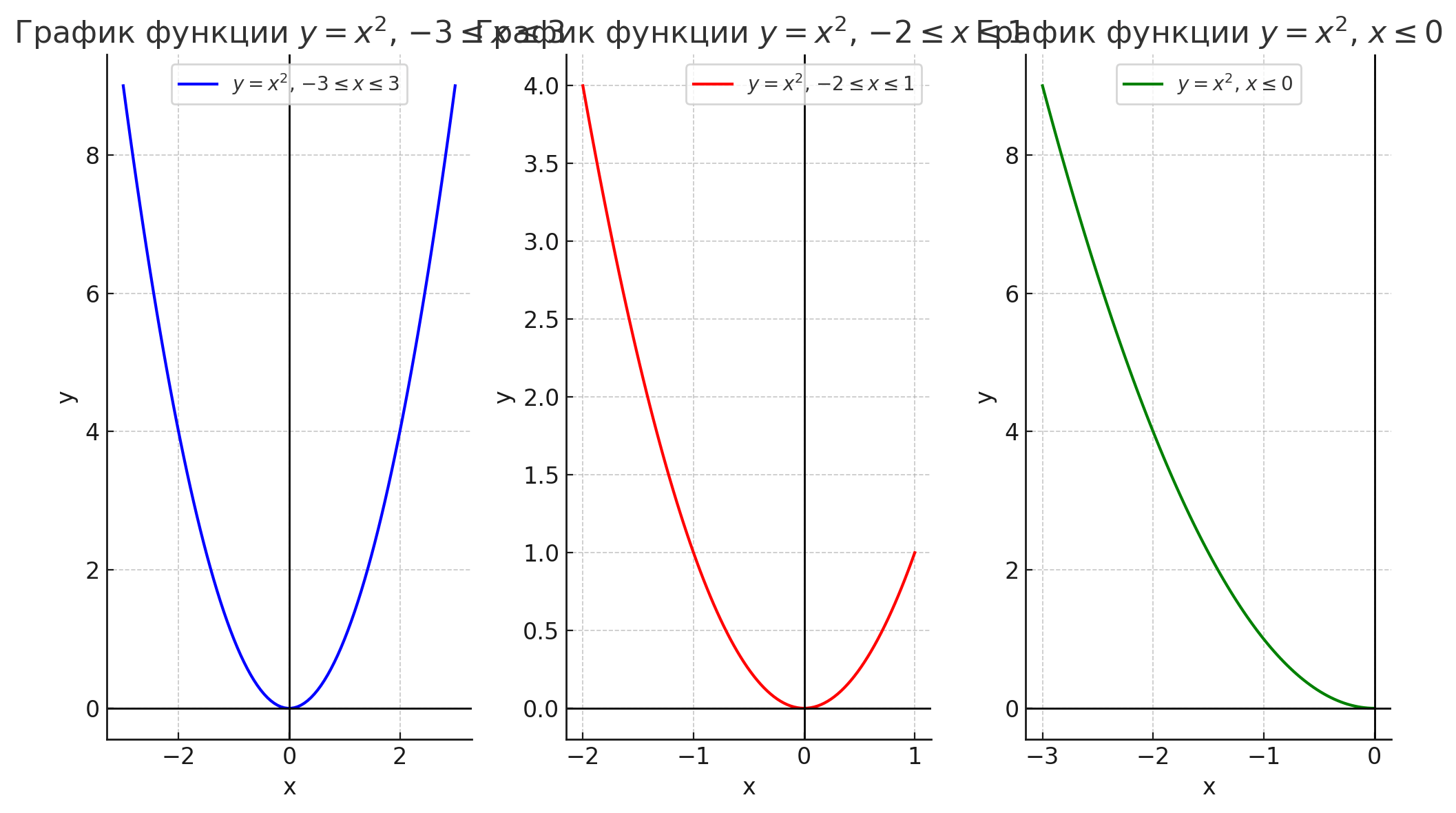
1. График функции \( y = x^2 \) для интервала \( -3 \leq x \leq 3 \) — синим цветом.
2. График функции \( y = x^2 \) для интервала \( -2 \leq x \leq 1 \) — красным цветом.
3. График функции \( y = x^2 \) для интервала \( x \leq 0 \) — зелёным цветом.
График функции \( y = x^2 \):
1. График функции \( y = x^2 \) для интервала \( -3 \leq x \leq 3 \) — синим цветом:
Этот график охватывает все значения \( x \) от -3 до 3, включая вершину параболы, которая находится в точке \( (0, 0) \), и симметричен относительно оси \( y \). Для положительных и отрицательных значений \( x \) значения \( y \) будут одинаковыми по модулю, так как функция квадратичная. График представляет собой стандартную параболу, направленную вверх. Это важно, поскольку квадратичные функции всегда имеют такую форму. График будет синим цветом, что помогает выделить этот интервал на фоне других графиков.
2. График функции \( y = x^2 \) для интервала \( -2 \leq x \leq 1 \) — красным цветом:
Этот график ограничивает область изменения \( x \) от -2 до 1. В пределах этого интервала график функции \( y = x^2 \) будет отображать часть параболы, которая начинается в точке \( (-2, 4) \) и заканчивается в точке \( (1, 1) \), проходя через вершину в начале координат. Использование красного цвета позволяет визуально выделить этот ограниченный интервал, что особенно полезно для выделения сегмента функции, когда интересует только часть всей параболы. Как и в первом случае, функция остается квадратичной, и значения \( y \) изменяются по закону квадрата.
3. График функции \( y = x^2 \) для интервала \( x \leq 0 \) — зелёным цветом:
Этот график охватывает только те значения \( x \), которые меньше или равны нулю. В этом случае график будет показывать только левую половину параболы, которая симметрична относительно оси \( y \). Начало графика будет в точке \( (0, 0) \), а далее значения \( y \) будут увеличиваться по мере увеличения отрицательных значений \( x \). Зеленый цвет помогает выделить только эту часть параболы, которая находится в отрицательной области \( x \). Этот интервал полезен, когда нужно изучить, как функция ведет себя при отрицательных значениях \( x \).
Все три графика будут представлять собой части одной и той же параболы, но каждый интервал выделен своим цветом для более удобного визуального восприятия. Это позволяет легче наблюдать за изменениями функции на разных отрезках, а также фокусировать внимание на определённых частях графика.