ГДЗ по Алгебре 7 Класс Номер 487 Дорофеев, Суворова — Подробные Ответы

Задача

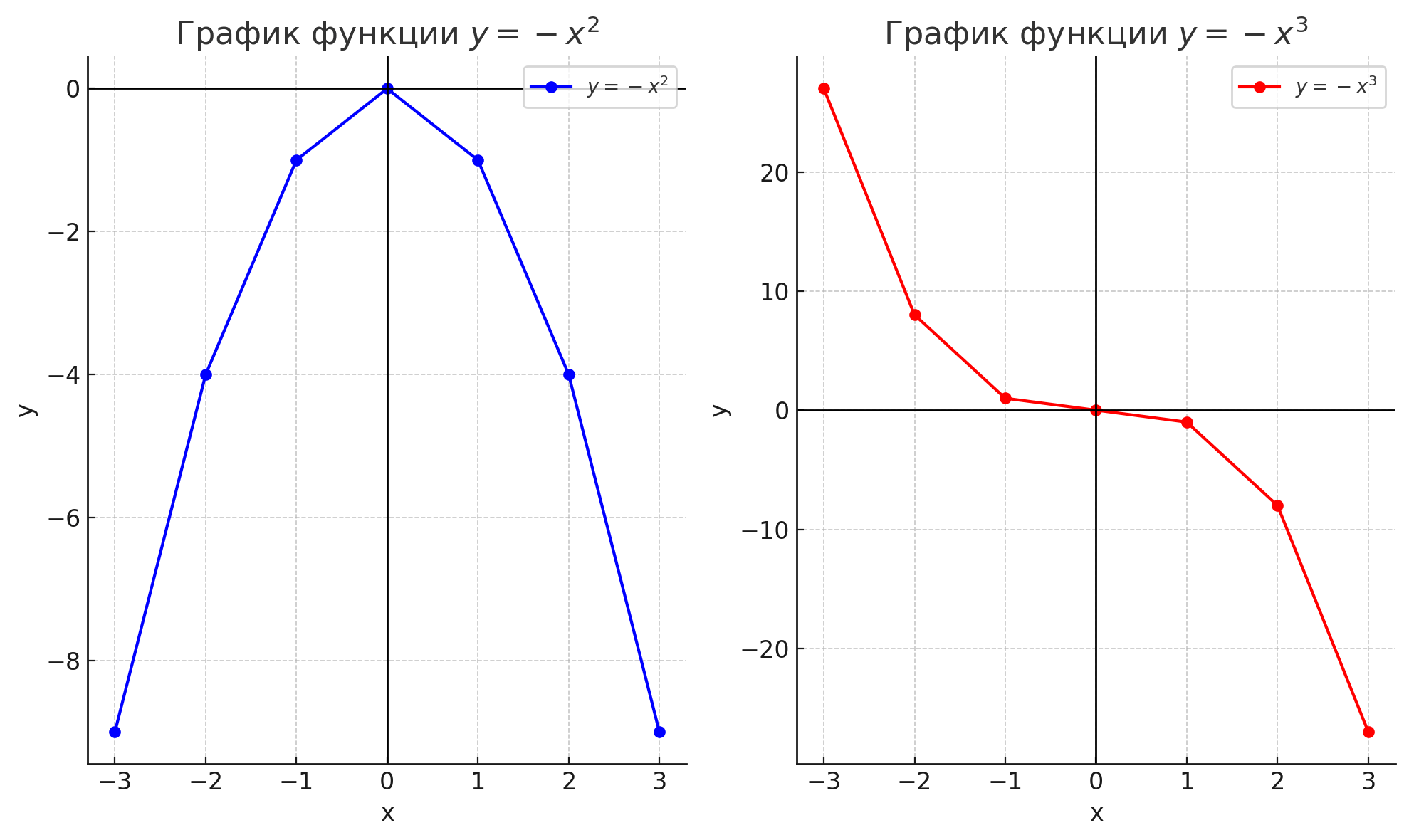
Постройте по точкам график зависимости: а) у = -х2; б) у = -х3.

Краткий ответ:

а) \( y = -x^2 \);

Функция \( y = -x^2 \) представляет собой параболу, которая направлена вниз. График этой функции симметричен относительно оси \( y \). Значения \( y \) вычисляются как отрицательные квадраты значений \( x \), то есть, чем дальше \( x \) от нуля, тем меньше становится значение \( y \). График функции выглядит как перевернутая парабола.

Точки для построения графика:

\( x = -3 \), \( y = -9 \)
\( x = -2 \), \( y = -4 \)
\( x = -1 \), \( y = -1 \)
\( x = 0 \), \( y = 0 \)
\( x = 1 \), \( y = -1 \)
\( x = 2 \), \( y = -4 \)
\( x = 3 \), \( y = -9 \)

б) \( y = -x^3 \);

Функция \( y = -x^3 \) представляет собой кубическую кривую. График этой функции проходит через начало координат и имеет два различных типа роста в зависимости от знака \( x \). При отрицательных значениях \( x \) \( y \) будет положительным, а при положительных значениях \( x \) — отрицательным. График этой функции не симметричен относительно оси \( y \).

Точки для построения графика:

\( x = -3 \), \( y = 27 \)
\( x = -2 \), \( y = 8 \)
\( x = -1 \), \( y = 1 \)
\( x = 0 \), \( y = 0 \)
\( x = 1 \), \( y = -1 \)
\( x = 2 \), \( y = -8 \)
\( x = 3 \), \( y = -27 \)

График функции \( y = -x^2 \) будет отображать параболу, направленную вниз, а график функции \( y = -x^3 \) будет изображать асимметричную кривую, проходящую через начало координат.

Подробный ответ:

а) \( y = -x^2 \);

Функция \( y = -x^2 \) представляет собой квадратичную зависимость, где \( y \) всегда отрицательно или равно нулю, так как выражение \( -x^2 \) всегда будет иметь отрицательные значения для всех значений \( x \), кроме \( x = 0 \), где \( y = 0 \). Это уравнение описывает параболу, направленную вниз, которая симметрична относительно оси \( y \), то есть график функции будет зеркально отражен относительно вертикальной оси. Важно отметить, что для всех значений \( x \), не равных нулю, функция всегда будет давать отрицательные значения.

График функции будет иметь форму параболы, вершина которой находится в начале координат. Для вычисления значений функции на графике мы подставляем различные значения \( x \) и вычисляем соответствующие значения \( y \):

\( x = -3 \), \( y = -(-3)^2 = -9 \)
\( x = -2 \), \( y = -(-2)^2 = -4 \)
\( x = -1 \), \( y = -(-1)^2 = -1 \)
\( x = 0 \), \( y = -(0)^2 = 0 \)
\( x = 1 \), \( y = -(1)^2 = -1 \)
\( x = 2 \), \( y = -(2)^2 = -4 \)
\( x = 3 \), \( y = -(3)^2 = -9 \)

Из приведенных точек мы видим, что для положительных и отрицательных значений \( x \) график будет иметь одинаковые значения по модулю, что подтверждает симметричность функции относительно оси \( y \). Это важная особенность всех квадратичных функций с отрицательным коэффициентом при \( x^2 \).

б) \( y = -x^3 \);

Функция \( y = -x^3 \) представляет собой кубическую зависимость, где \( y \) изменяется несимметрично относительно оси \( y \). В отличие от квадратичной функции, здесь значения \( y \) будут положительными для отрицательных значений \( x \) и отрицательными для положительных значений \( x \), и наоборот. Таким образом, функция будет иметь S-образную форму с симметрией относительно начала координат (точки \( (0; 0) \)) и изменяющимся наклоном по мере увеличения значения \( x \).

Для построения графика функции \( y = -x^3 \) можно подставить различные значения \( x \) и вычислить соответствующие значения \( y \), например:

\( x = -3 \), \( y = -(-3)^3 = 27 \)
\( x = -2 \), \( y = -(-2)^3 = 8 \)
\( x = -1 \), \( y = -(-1)^3 = 1 \)
\( x = 0 \), \( y = -(0)^3 = 0 \)
\( x = 1 \), \( y = -(1)^3 = -1 \)
\( x = 2 \), \( y = -(2)^3 = -8 \)
\( x = 3 \), \( y = -(3)^3 = -27 \)

Как видно из приведенных точек, при \( x = -3 \) и \( x = 3 \) значения \( y \) различаются по знаку (положительные для отрицательных значений \( x \) и отрицательные для положительных значений \( x \)). Это является важной характеристикой всех кубических функций с отрицательным коэффициентом при \( x^3 \), где знак зависит от величины \( x \).

График функции \( y = -x^3 \) имеет характерную S-образную форму, и его наклон меняется от положительного к отрицательному по мере увеличения значения \( x \), что также характеризует кубические функции с отрицательным коэффициентом.

Таким образом, для обеих функций графики имеют следующие особенности:

Функция \( y = -x^2 \) — парабола, направленная вниз, симметрична относительно оси \( y \), всегда отрицательна для \( x \neq 0 \).
Функция \( y = -x^3 \) — кубическая кривая, с S-образной формой, меняет знак в зависимости от знака \( x \), проходя через начало координат.

Оцени решение