ГДЗ по Алгебре 7 Класс Номер 485 Дорофеев, Суворова — Подробные Ответы

Задача

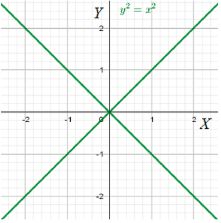
Постройте множество точек плоскости, координаты которых связаны соотношением у2 = х2.

Краткий ответ:

\(y^2 = x^2\)

\(|y| = |x|\)

\[
\left\{
\begin{array}{ll}
y = x, & y \geq 0 \\
y = -x, & y < 0
\end{array}
\right.
\]

Подробный ответ:

Уравнение \( y^2 = x^2 \) задает зависимость между переменными \( y \) и \( x \), при которой значения этих переменных могут быть как положительными, так и отрицательными. Это уравнение подразумевает, что квадрат обеих переменных равен, следовательно, их модули одинаковы, то есть \( |y| = |x| \).

Следовательно, можно выделить два возможных случая для функции \( y(x) \):

\[
\left\{
\begin{array}{ll}
y = x, & \text{если } y \geq 0 \\
y = -x, & \text{если } y < 0
\end{array}
\right.
\]

Таким образом, решение уравнения \( y^2 = x^2 \) сводится к разбиению на два случая: первый случай, где \( y \) равно \( x \), когда \( y \geq 0 \), и второй, где \( y \) равно \( -x \), когда \( y < 0 \). Это отражает геометрическое представление двух прямых на координатной плоскости, которые пересекаются в начале координат, и их графики симметричны относительно оси абсцисс.

Оцени решение