ГДЗ по Алгебре 7 Класс Номер 484 Дорофеев, Суворова — Подробные Ответы
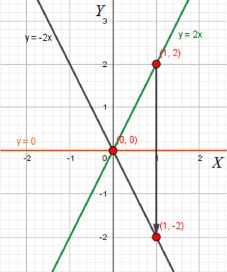
Известно, что график зависимости у = 2х — прямая. Постройте эту прямую по точкам. (Сколько точек для этого достаточно?) Постройте прямую, симметричную относительно оси абсцисс прямой у = 2х. Найдите зависимость, которой удовлетворяют координаты точек этой прямой.
Дано уравнение прямой: \( y = 2x \). Для её построения достаточно двух точек. Например:
- Для \( x = 0 \), \( y = 0 \) (точка \( (0, 0) \)).
- Для \( x = 1 \), \( y = 2 \) (точка \( (1, 2) \)).
Построим симметричную прямую относительно оси абсцисс, изменив знак у \( y \): \( y = -2x \).
- Для \( x = 0 \), \( y = 0 \) (точка \( (0, 0) \)).
- Для \( x = 1 \), \( y = -2 \) (точка \( (1, -2) \)).
Дано уравнение прямой: \( y = 2x \). Эта прямая является линейной, и для её построения достаточно двух точек.
Для нахождения двух точек, достаточно подставить любые два значения \( x \) и найти соответствующие значения \( y \). Например:
- Для \( x = 0 \), подставляем в уравнение \( y = 2 \cdot 0 = 0 \). Первая точка: \( (0, 0) \).
- Для \( x = 1 \), подставляем в уравнение \( y = 2 \cdot 1 = 2 \). Вторая точка: \( (1, 2) \).
Теперь, зная две точки \( (0, 0) \) и \( (1, 2) \), мы можем построить прямую, проходящую через эти точки.
Построение симметричной прямой относительно оси абсцисс:
Чтобы построить прямую, симметричную относительно оси абсцисс, необходимо изменить знак у переменной \( y \). То есть для прямой \( y = 2x \) симметричная прямая будет иметь уравнение:
\( y = -2x \)
Теперь подставим те же значения \( x \) для симметричной прямой:
- Для \( x = 0 \), подставляем в уравнение \( y = -2 \cdot 0 = 0 \). Первая точка: \( (0, 0) \).
- Для \( x = 1 \), подставляем в уравнение \( y = -2 \cdot 1 = -2 \). Вторая точка: \( (1, -2) \).
Таким образом, для симметричной прямой относительно оси абсцисс, уравнение будет \( y = -2x \), и для её построения также достаточно двух точек: \( (0, 0) \) и \( (1, -2) \).