ГДЗ по Алгебре 7 Класс Номер 483 Дорофеев, Суворова — Подробные Ответы
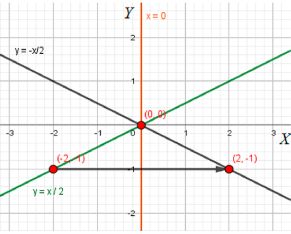
На рисунке 5.32, а изображена прямая, которая является графиком зависимости \( y = \frac{1}{2}x \) (см. задание 482). Перенесите этот рисунок в тетрадь и постройте в той же системе координат прямую, симметричную этой прямой относительно оси ординат. Найдите зависимость, связывающую координаты точек построенной прямой, и задайте её алгебраически.
Дано уравнение прямой: \( y = \frac{1}{2}x \). Чтобы найти симметричную прямую относительно оси ординат, заменим \( x \) на \( -x \), получив уравнение \( y = -\frac{1}{2}x \). Это и есть симметричная прямая.
Итак, зависимость для симметричной прямой: \( y = -\frac{1}{2}x \).
Для решения этого задания давайте пошагово разберем, как найти зависимость для симметричной прямой относительно оси ординат и ее алгебраическое выражение.
- Начальное уравнение прямой:
Дано уравнение прямой:\( y = \frac{1}{2}x \)Это прямая, которая проходит через начало координат и имеет угловой коэффициент \( \frac{1}{2} \). Прямая наклонена вверх, так как угловой коэффициент положительный.
- Построение симметричной прямой относительно оси ординат:
Чтобы построить симметричную прямую относительно оси ординат (оси \( y \)), нам нужно изменить знак у переменной \( x \). То есть для симметричной прямой в уравнении \( y = \frac{1}{2}x \) необходимо заменить \( x \) на \( -x \):\( y = \frac{1}{2}(-x) = -\frac{1}{2}x \)Это уравнение прямой, которая симметрична исходной относительно оси \( y \).
- Алгебраическая зависимость:
Таким образом, уравнение симметричной прямой, которое связывает координаты точек на этой прямой, будет следующим:\( y = -\frac{1}{2}x \)Это прямая с угловым коэффициентом \( -\frac{1}{2} \), что означает, что прямая наклонена вниз.
- Результат:
Зависимость, связывающая координаты точек симметричной прямой, это:\( y = -\frac{1}{2}x \)
Таким образом, вы можете нарисовать обе прямые: исходную \( y = \frac{1}{2}x \) и её симметричную относительно оси ординат \( y = -\frac{1}{2}x \).