ГДЗ по Алгебре 7 Класс Номер 482 Дорофеев, Суворова — Подробные Ответы
а) Таблица:
| x | -2 | -1 | 0 | 1 | |
| y | -1 | -0.5 | 0 | 0.5 | 1 |
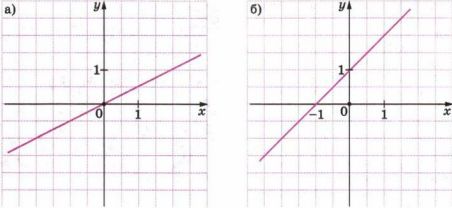
\( x = 2y, \quad y = \frac{1}{2}x \).
б) Таблица:
| x | -2 | -1 | 0 | 1 |
| y | -1 | 0 | 1 | 2 |
\( y — x = 1, \quad y = 1 + x \).
а) Таблица:
| x | -2 | -1 | 0 | 1 | |
| y | -1 | -0.5 | 0 | 0.5 | 1 |
В данной задаче рассматриваются два взаимосвязанных уравнения:
первое, \( x = 2y \), задает зависимость между переменными \( x \) и \( y \), при этом переменная \( x \) в два раза больше переменной \( y \).
Второе уравнение, \( y = \frac{1}{2}x \), показывает, что переменная \( y \) является половиной от значения переменной \( x \).
Для каждой из этих переменных были вычислены значения, которые приведены в таблице. Таким образом, значения переменной \( y \) рассчитаны для различных значений \( x \) согласно данным уравнениям. Таблица демонстрирует, как изменяется значение \( y \) при изменении \( x \).
б) Таблица:
| x | -2 | -1 | 0 | 1 |
| y | -1 | 0 | 1 | 2 |
Во втором случае мы имеем два других уравнения, которые связывают \( x \) и \( y \):
первое, \( y — x = 1 \), определяет разницу между переменными \( y \) и \( x \), которая всегда равна 1.
Это означает, что значение \( y \) на 1 больше, чем значение \( x \).
Второе уравнение, \( y = 1 + x \), является прямой зависимостью, где значение \( y \) всегда больше значения \( x \) на 1.
Все возможные значения переменной \( y \) вычислены для заданных значений \( x \) и отображены в таблице. Таким образом, можно увидеть, как переменная \( y \) изменяется относительно \( x \), при этом соблюдается линейная зависимость.