ГДЗ по Алгебре 7 Класс Номер 480 Дорофеев, Суворова — Подробные Ответы
Задайте на алгебраическом языке и изобразите на координатной плоскости множество точек, у которых:
а) ордината равна утроенной абсциссе;
б) ордината на 3 больше абсциссы;
в) абсцисса на 2 больше ординаты;
г) сумма абсциссы и ординаты равна 4.
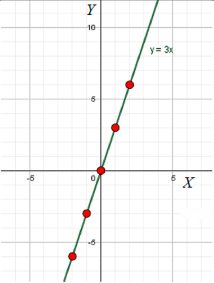
а) Ордината равна утроенной абсциссе:
y = 3x
График этой функции представляет собой прямую, проходящую через начало координат с угловым коэффициентом 3.
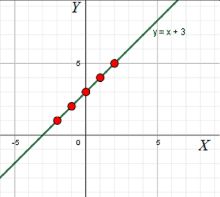
б) Ордината на 3 больше абсциссы:
y = x + 3
График этой функции также представляет собой прямую, но с угловым коэффициентом 1 и сдвигом на 3 единицы вверх.
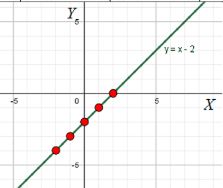
в) Абсцисса на 2 больше ординаты:
x = y + 2
График будет вертикальной прямой, которая пересекает ось абсцисс в точке x = 2.
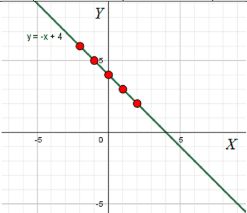
г) Сумма абсциссы и ординаты равна 4:
x + y = 4
График этой функции представляет собой прямую, которая проходит через точки (4,0) и (0,4), с угловым коэффициентом -1.
а) Ордината равна утроенной абсциссе:
Алгебраически это можно записать как: y = 3x. Это линейная функция, которая определяет зависимость между ординатой и абсциссой, где ордината (y) является утроенной величиной абсциссы (x). Графически эта функция представляет собой прямую, которая проходит через начало координат (0, 0) и имеет угловой коэффициент, равный 3. Это означает, что на каждый шаг по оси абсцисс, значение функции увеличивается в три раза быстрее. Такая функция будет расти с наклоном, направленным вверх, при этом её график будет стремиться вверх быстрее, чем график функции с меньшим угловым коэффициентом.
б) Ордината на 3 больше абсциссы:
Алгебраически это выражается следующим образом: y = x + 3. Эта линейная функция также имеет угловой коэффициент, равный 1, что означает, что с каждым увеличением абсциссы на 1, ордината увеличивается на 1. Однако здесь есть постоянное смещение, равное 3, что сдвигает график функции на 3 единицы вверх по оси Y. Это означает, что график прямой будет пересекать ось ординат в точке (0, 3), и в дальнейшем будет идти с наклоном 45 градусов вверх, образуя прямую с угловым коэффициентом 1.
в) Абсцисса на 2 больше ординаты:
В данном случае, если абсцисса на 2 больше ординаты, то алгебраически это выражается как: x = y + 2. Мы можем переписать это уравнение в более стандартную форму, получив: y = x — 2. Это также линейная функция, но теперь её график будет сдвинут вниз на 2 единицы. Эта прямая будет пересекать ось абсцисс в точке (2, 0), а ось ординат – в точке (0, -2). График будет наклонён вниз, так как угловой коэффициент равен 1, и будет иметь постоянное смещение вдоль оси Y.
г) Сумма абсциссы и ординаты равна 4:
Алгебраически это можно записать как: x + y = 4. Это уравнение также представляет собой прямую, но с угловым коэффициентом -1. Это означает, что для каждого увеличения абсциссы на 1, ордината уменьшается на 1. График этой функции будет пересекать оси координат в точках (4, 0) и (0, 4). Это прямая с наклоном вниз, которая равномерно спускается по мере увеличения абсциссы. График этой функции образует угол 45 градусов с осями, но направлен вниз.