ГДЗ по Алгебре 7 Класс Номер 479 Дорофеев, Суворова — Подробные Ответы
Постройте по точкам график зависимости, заданной равенством: а) у = -2х; б) у = 2-х; в) у — х = 3.
Подсказка. В каждом случае составьте таблицу значений х и у. В случае в удобно сначала выразить у через х: у = х + 3.
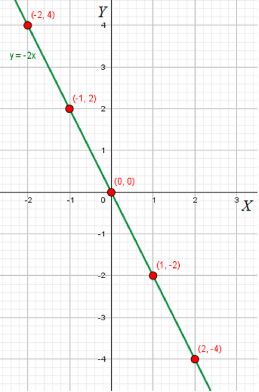
а) \( y = -2x \)
Для этой функции составим таблицу значений \( x \) и соответствующих значений \( y \):
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|---|---|
| y | 6 | 4 | 2 | 0 | -2 | -4 | -6 |
График функции \( y = -2x \) представляет собой прямую, которая проходит через вычисленные точки, и имеет отрицательный наклон.
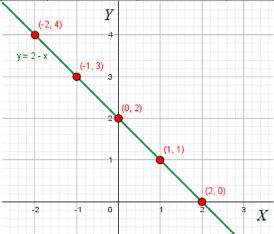
б) \( y = 2 — x \)
Для этой функции составим таблицу значений \( x \) и соответствующих значений \( y \):
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|---|---|
| y | 5 | 4 | 3 | 2 | 1 | 0 | -1 |
График функции \( y = 2 — x \) также является прямой, но с наклоном, противоположным первому графику.
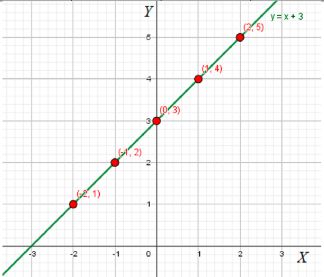
в) \( y = x + 3 \)
Для этой функции составим таблицу значений \( x \) и соответствующих значений \( y \):
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|---|---|
| y | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
График функции \( y = x + 3 \) также является прямой, и её наклон положительный, так как при увеличении \( x \), значение \( y \) увеличивается.
Графики этих зависимостей представляют собой прямые, и на каждом из них значения \( y \) изменяются линейно в зависимости от \( x \). Все три графика показывают прямые линии с разным наклоном, отображающие различные линейные зависимости.
а) \( y = -2x \)
Эта зависимость описывает линейную функцию с отрицательным коэффициентом при \( x \), что означает, что график будет убывающим, то есть при увеличении значения \( x \), значение \( y \) будет уменьшаться. Мы составляем таблицу значений \( x \) и соответствующих значений \( y \) для разных точек:
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|---|---|
| y | 6 | 4 | 2 | 0 | -2 | -4 | -6 |
Как видно из таблицы, значения \( y \) уменьшаются, когда \( x \) увеличивается, что подтверждает, что график функции имеет отрицательный наклон. График функции будет прямой, которая проходит через эти вычисленные точки.
График функции \( y = -2x \) пересекает ось \( y \) в точке \( y = 0 \), так как при \( x = 0 \), \( y = 0 \). Это также означает, что график функции является прямой с угловым коэффициентом -2. Эта прямая проходит через все точки, вычисленные в таблице, и представляет собой линейную зависимость между переменными \( x \) и \( y \).
б) \( y = 2 — x \)
Эта зависимость также описывает линейную функцию, но с противоположным наклоном по сравнению с первой функцией. Угловой коэффициент равен -1, что означает, что график будет наклонен вниз. Мы также составляем таблицу значений \( x \) и соответствующих значений \( y \):
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|---|---|
| y | 5 | 4 | 3 | 2 | 1 | 0 | -1 |
Как видно из таблицы, при увеличении значения \( x \) значение \( y \) уменьшается, что подтверждает наклон графика вниз. График этой функции также будет прямой, но с угловым коэффициентом -1.
График функции \( y = 2 — x \) пересекает ось \( y \) в точке \( y = 2 \), так как при \( x = 0 \), \( y = 2 \). Это также означает, что прямая будет иметь наклон в сторону оси \( x \), но с меньшим углом по сравнению с первой функцией.
в) \( y = x + 3 \)
Это также линейная функция, но с положительным наклоном. Угловой коэффициент равен 1, что означает, что график будет возрастать. Мы составляем таблицу значений для данной функции:
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|---|---|
| y | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
При увеличении \( x \), значение \( y \) увеличивается, что подтверждает положительный наклон графика. График функции \( y = x + 3 \) пересекает ось \( y \) в точке \( y = 3 \), так как при \( x = 0 \), \( y = 3 \).
Эта прямая будет иметь угловой коэффициент 1, что означает, что график будет идти вверх с углом наклона 45 градусов относительно оси \( x \). Он будет проходить через все вычисленные точки, и его можно будет построить, соединяя эти точки.
Графики этих функций являются прямыми, так как функции линейные. Эти прямые имеют различные угловые коэффициенты, которые определяют их наклон. В первом случае график убывающий (отрицательный наклон), во втором — также убывающий, но с меньшим наклоном, и в третьем случае график возрастает (положительный наклон).