ГДЗ по Алгебре 7 Класс Номер 476 Дорофеев, Суворова — Подробные Ответы
1) Постройте график зависимости
\( y = x + 2 \). Для этого:
Вычислите значения \( y \) для указанных значений \( x \) и заполните таблицу:
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|---|---|---|---|
| y | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
Постройте точки, координаты которых занесены в таблицу.
Если вы всё сделали аккуратно, то все точки будут лежать на одной прямой.
Проведите эту прямую с помощью линейки.
Задача: Построить график функции \( y = x + 2 \).
Для этого мы вычислили значения \( y \) для заданных значений \( x \) в диапазоне от -4 до 4. Полученная таблица значений:
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|---|---|---|---|
| y | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
График функции \( y = x + 2 \) представляет собой прямую, проходящую через все эти точки. Прямая отображает линейную зависимость, где каждое значение \( y \) увеличивается на 1 при увеличении \( x \) на 1.
График был построен, и вы можете увидеть прямую линию, которая проходит через все вычисленные точки.
Задача: Построить график функции \( y = x + 2 \).
Функция \( y = x + 2 \) является линейной, и её график представляет собой прямую. Для этого мы вычислили значения \( y \) для ряда значений \( x \) от -4 до 4, подставляя каждое значение \( x \) в уравнение \( y = x + 2 \). Полученная таблица значений для функции:
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|---|---|---|---|
| y | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
Каждое значение \( y \) соответствует точке на графике, и все эти точки лежат на одной прямой. Это связано с тем, что функция \( y = x + 2 \) является линейной функцией, где коэффициент при \( x \) равен 1, что означает, что с увеличением значения \( x \) на 1, значение \( y \) увеличивается на 1. Это свойство линейных функций приводит к образованию прямой, которая проходит через все вычисленные точки.
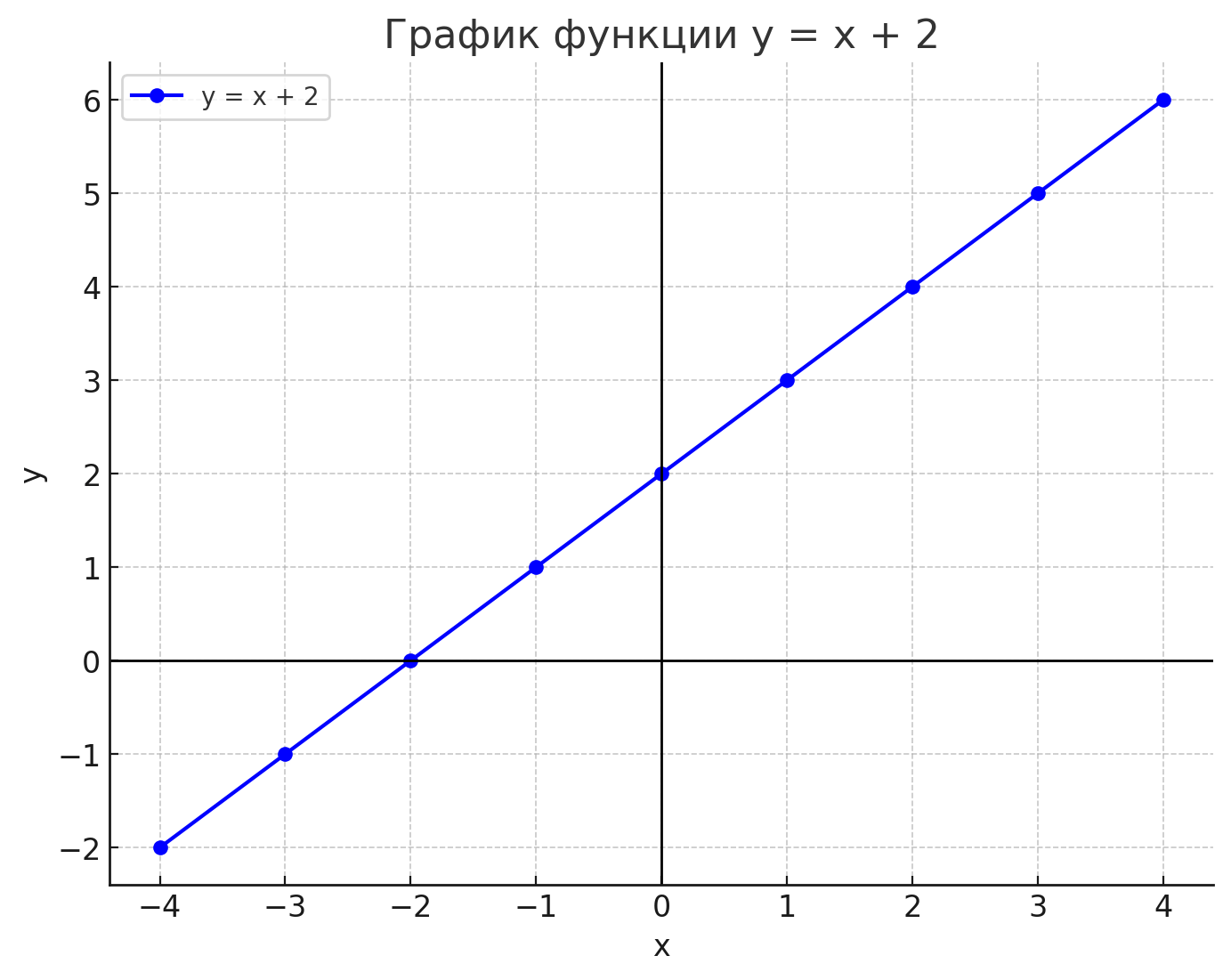
График функции \( y = x + 2 \) будет прямой, проходящей через точки с координатами, вычисленными в таблице. Визуально эта прямая будет пересекать ось \( y \) в точке \( y = 2 \), так как при \( x = 0 \), \( y = 2 \). Таким образом, график функции будет иметь угол наклона 45 градусов относительно оси \( x \), так как коэффициент при \( x \) равен 1.
Для построения графика можно нарисовать прямую, соединяя все вычисленные точки. Эта прямая будет проходить через следующие точки: \( (-4, -2) \), \( (-3, -1) \), \( (-2, 0) \), \( (-1, 1) \), \( (0, 2) \), \( (1, 3) \), \( (2, 4) \), \( (3, 5) \), \( (4, 6) \).
Визуально график будет выглядеть как прямая линия, которая начинает свой путь в нижнем левом углу и постепенно поднимется вверх вправо, проходя через все точки, как показано в таблице. Эта прямая является графиком функции \( y = x + 2 \), которая имеет постоянный наклон и выражает прямолинейную зависимость между \( x \) и \( y \).
График был построен, и вы можете увидеть прямую линию, которая проходит через все вычисленные точки. Такой график характерен для линейных функций, где зависимость между переменными \( x \) и \( y \) всегда сохраняется постоянной. Он помогает наглядно продемонстрировать, как изменения \( x \) влияют на \( y \), и является основным примером линейной функции в алгебре.