ГДЗ по Алгебре 7 Класс Номер 475 Дорофеев, Суворова — Подробные Ответы
Изобразите на координатной плоскости и опишите на алгебраическом языке множество точек, симметричных относительно оси абсцисс точкам полосы, заданной неравенством 2 < = у < = 5.
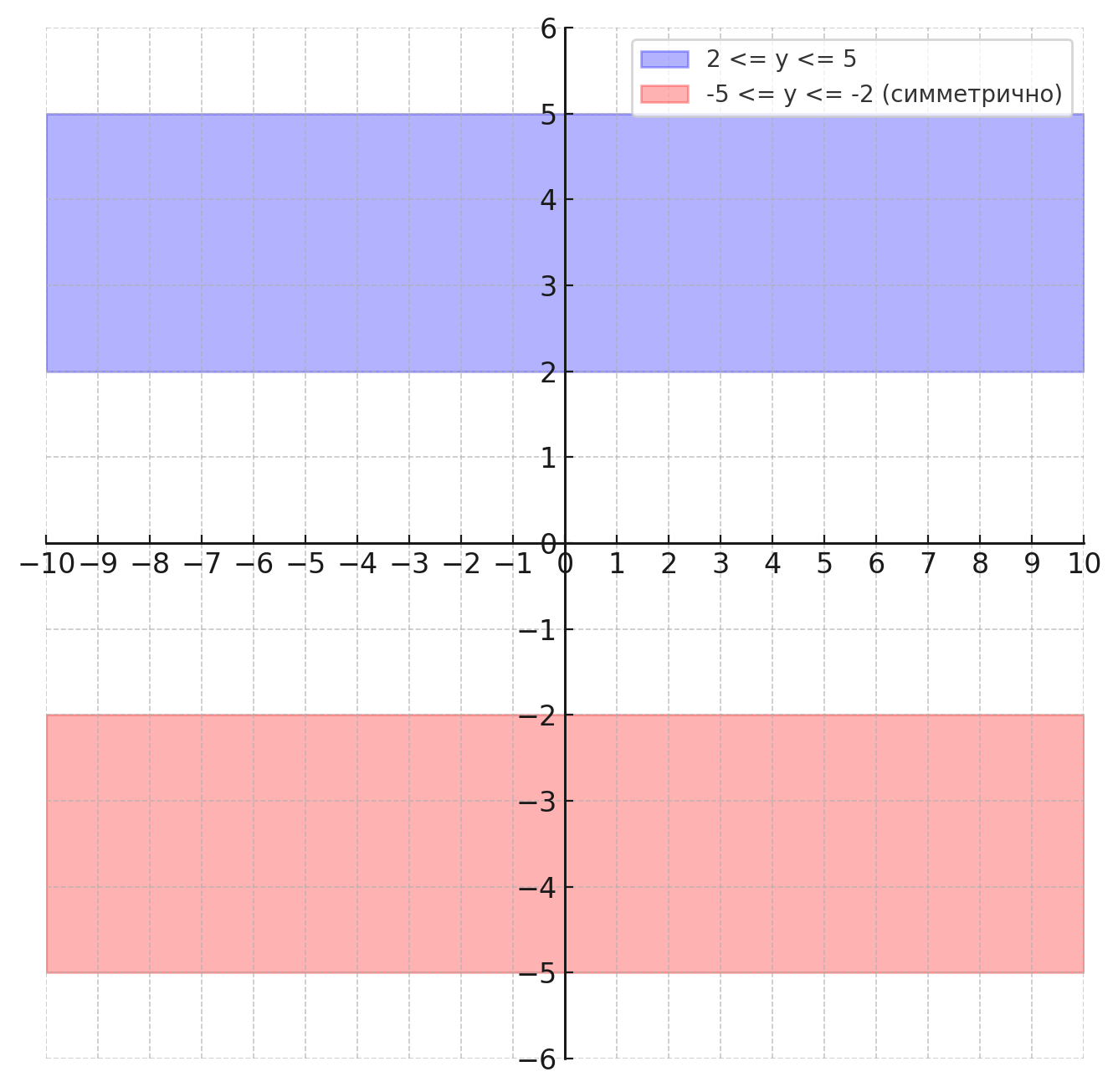
Полоса, заданная неравенством \( 2 \leq y \leq 5 \), представляет собой область между двумя горизонтальными прямыми \( y = 2 \) и \( y = 5 \), включая сами эти прямые. Все точки, расположенные между этими прямыми, удовлетворяют данному условию. Это горизонтальная полоса на координатной плоскости, где значения по оси \( y \) лежат в пределах от 2 до 5.
Симметричные точки относительно оси абсцисс будут иметь такие же координаты по оси \( x \), но с противоположными знаками по оси \( y \). Если точка \( P(x, y) \) лежит в полосе \( 2 \leq y \leq 5 \), то её симметричная точка \( P'(x, -y) \) будет находиться в области \( -5 \leq y \leq -2 \). Таким образом, множество симметричных точек будет располагаться между двумя горизонтальными прямыми \( y = -2 \) и \( y = -5 \), включая эти прямые.
Алгебраически, множество симметричных точек можно описать как: \( 2 \leq y \leq 5 \Rightarrow -5 \leq y \leq -2 \).
Полоса, заданная неравенством \( 2 \leq y \leq 5 \), представляет собой прямоугольную область, расположенную между двумя горизонтальными прямыми: одна из которых проходит через точку \( y = 2 \), а другая — через точку \( y = 5 \). Эти прямые включены в область, так как неравенства \( \leq \) и \( \geq \) допускают включение самих этих значений. Таким образом, все точки, для которых значение \( y \) лежит в пределах от 2 до 5, а \( x \)-координата может быть любым, принадлежат этой полосе. Геометрически это означает, что область, заданная неравенством \( 2 \leq y \leq 5 \), представляет собой горизонтальную полосу на координатной плоскости, ограниченную двумя прямыми. Все точки на и между этими прямыми составляют множество точек, удовлетворяющих условию.
Симметрия относительно оси абсцисс означает, что для каждой точки в области \( 2 \leq y \leq 5 \) её симметричная точка будет располагаться с противоположным знаком по оси \( y \), но с тем же значением по оси \( x \). Если точка \( P(x, y) \) лежит в полосе \( 2 \leq y \leq 5 \), то её симметричная точка \( P'(x, -y) \) будет находиться в области \( -5 \leq y \leq -2 \). То есть, для каждой точки на прямой \( y = 2 \), её симметричная точка будет располагаться на прямой \( y = -2 \), а для каждой точки на прямой \( y = 5 \), симметричная точка будет на прямой \( y = -5 \). Все такие точки лежат в горизонтальной полосе, ограниченной прямыми \( y = -5 \) и \( y = -2 \), и эти прямые включены в область, так как неравенства \( \leq \) и \( \geq \) допускают включение самих этих значений.
Алгебраически симметричные точки для множества, заданного условием \( 2 \leq y \leq 5 \), можно описать следующим образом: если точка \( P(x, y) \) принадлежит полосе, то её симметричная точка \( P'(x, -y) \) будет принадлежать области, заданной неравенством \( -5 \leq y \leq -2 \). Таким образом, множество симметричных точек будет расположено между двумя горизонтальными прямыми \( y = -2 \) и \( y = -5 \), включая эти прямые.