ГДЗ по Алгебре 7 Класс Номер 474 Дорофеев, Суворова — Подробные Ответы

Постройте на координатной плоскости и опишите на алгебраическом языке прямую, симметричную точкам прямой х = 3:
а) относительно оси ординат;
б) относительно прямой х = 1.

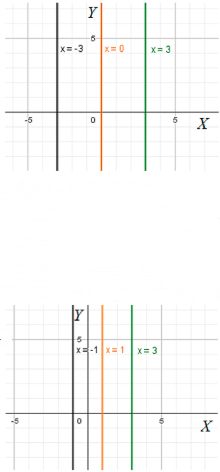
а) \( x = 3 \) — это вертикальная прямая, проходящая через точку \( x = 3 \) на оси \( x \). Симметричная прямая относительно оси ординат будет расположена на таком же расстоянии от оси \( y \), но с противоположным знаком по оси \( x \). Таким образом, симметричная прямая будет проходить через точку \( x = -3 \), и её уравнение будет записано как \( x = -3 \). Это вертикальная прямая, симметричная относительно оси ординат.

б) \( x = 3 \) — это вертикальная прямая, проходящая через точку \( x = 3 \) на оси \( x \). Симметричная прямая относительно прямой \( x = 1 \) будет находиться на таком же расстоянии от прямой \( x = 1 \), но в другую сторону. Так как расстояние от прямой \( x = 1 \) до \( x = 3 \) равно 2, то симметричная прямая будет находиться на расстоянии 2 единиц влево от прямой \( x = 1 \), то есть на прямой \( x = -1 \). Это вертикальная прямая, симметричная относительно прямой \( x = 1 \).

а) \( x = 3 \) — это вертикальная прямая, которая проходит через точку \( x = 3 \) на оси \( x \) и параллельна оси \( y \). Прямая \( x = 3 \) представляет собой набор всех точек на координатной плоскости, у которых значение \( x \) равно 3, а значение \( y \) может быть любым. Это вертикальная линия, которая не пересекает ось \( x \), так как её координата по оси \( x \) фиксирована и равна 3. Симметричная прямая относительно оси ординат будет находиться на таком же расстоянии от оси \( y \), но с противоположным знаком по оси \( x \). Таким образом, симметричная прямая будет проходить через точку \( x = -3 \), и её уравнение будет записано как \( x = -3 \). Это также вертикальная прямая, расположенная симметрично по отношению к оси \( y \) и делящая плоскость на две части, с противоположными знаками по оси \( x \).

б) \( x = 3 \) — это вертикальная прямая, которая проходит через точку \( x = 3 \) на оси \( x \). Чтобы найти симметричную прямую относительно прямой \( x = 1 \), нужно учесть, что эта прямая будет располагаться на таком же расстоянии от прямой \( x = 1 \), но в противоположную сторону. Геометрически, если расстояние от прямой \( x = 1 \) до прямой \( x = 3 \) равно 2, то симметричная прямая будет расположена на таком же расстоянии, но в другую сторону от прямой \( x = 1 \). Таким образом, симметричная прямая будет расположена на прямой \( x = -1 \), что соответствует симметрии относительно прямой \( x = 1 \). Прямая \( x = -1 \) — это вертикальная линия, которая проходит через точку \( x = -1 \) на оси \( x \), и она симметрична прямой \( x = 3 \) относительно прямой \( x = 1 \). Таким образом, уравнение симметричной прямой будет записано как \( x = -1 \), и эта прямая будет параллельна оси \( y \).