ГДЗ по Алгебре 7 Класс Номер 473 Дорофеев, Суворова — Подробные Ответы

Изобразите на координатной плоскости множество точек, заданное условиями:
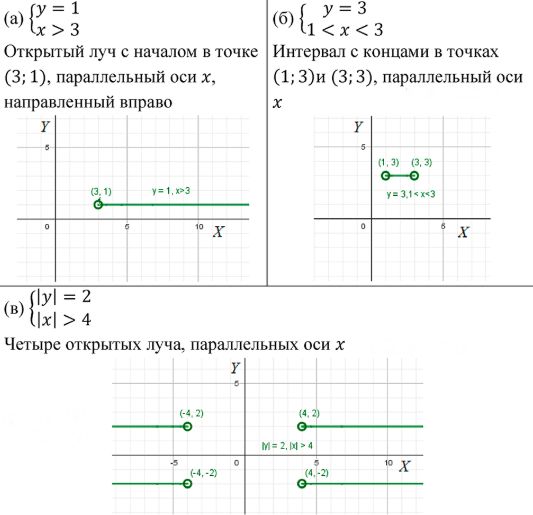
а) у = 1 и x > 3;
б) у = 3 и 1 < х < 3;
в) |у| = 2 и |х| > 4.

а) \( y = 1 \) и \( x > 3 \) — это прямая \( y = 1 \), но только те точки на ней, для которых \( x > 3 \). То есть, мы имеем горизонтальную прямую, но только правее точки \( x = 3 \).

б) \( y = 3 \) и \( 1 < x < 3 \) — это горизонтальная часть прямой \( y = 3 \), ограниченная между точками \( x = 1 \) и \( x = 3 \). Это будет отрезок на горизонтальной прямой \( y = 3 \), где \( x \) варьируется от 1 до 3.

в) \( |y| = 2 \) и \( |x| > 4 \) — это две горизонтальные прямые \( y = 2 \) и \( y = -2 \), но только те точки, для которых \( |x| > 4 \), то есть \( x < -4 \) или \( x > 4 \). Это будет два отрезка на этих горизонтальных прямых, ограниченных вертикальными прямыми \( x = -4 \) и \( x = 4 \).

а) \( y = 1 \) и \( x > 3 \) — это прямая, расположенная на уровне \( y = 1 \), но с дополнительным ограничением по \( x \), которое гласит, что \( x \) должно быть больше 3. Геометрически это означает, что мы имеем горизонтальную прямую, которая проходит через все точки, где \( y = 1 \), но она начинается от точки \( x = 3 \) и продолжается вправо, то есть все точки, для которых \( x > 3 \), принадлежат множеству. Важно отметить, что точка \( x = 3 \) не включена в область, так как неравенство строгое. Таким образом, эта область охватывает все точки, расположенные на прямой \( y = 1 \) правее точки \( x = 3 \), и все эти точки будут удовлетворять условию.

б) \( y = 3 \) и \( 1 < x < 3 \) — это часть горизонтальной прямой \( y = 3 \), но только те точки на ней, для которых \( x \) лежит в интервале от 1 до 3, не включая сами эти значения. Это значит, что рассматриваемая область представляет собой отрезок на горизонтальной прямой \( y = 3 \), ограниченный точками \( x = 1 \) и \( x = 3 \). Все точки, которые находятся между этими двумя значениями по оси \( x \), принадлежат этому множеству. Точки на самой прямой \( y = 3 \), где \( x \) строго между 1 и 3, составляют решение данного неравенства. Прямая \( y = 3 \) будет пересечена только в точках, где \( x \) находится в этом интервале.

в) \( |y| = 2 \) и \( |x| > 4 \) — это две горизонтальные прямые, одна из которых \( y = 2 \), а другая \( y = -2 \). Эти прямые ограничены дополнительными условиями для \( x \), которые задают область, расположенную за пределами вертикальных прямых \( x = -4 \) и \( x = 4 \). То есть, рассматриваемые прямые, \( y = 2 \) и \( y = -2 \), ограничены так, что только те точки, для которых \( |x| > 4 \), удовлетворяют условию. Это означает, что нам нужно рассматривать две области: слева от \( x = -4 \) и справа от \( x = 4 \). Таким образом, множество точек состоит из двух отрезков на горизонтальных прямых \( y = 2 \) и \( y = -2 \), которые ограничены вертикальными прямыми \( x = -4 \) и \( x = 4 \), но эти прямые не включаются в область.