ГДЗ по Алгебре 7 Класс Номер 472 Дорофеев, Суворова — Подробные Ответы

Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют условиям:
а) |x| = 3;
б) |у| = 1;
в) |у| < =2;
г) |х| > = 5;
д) |x| < = 3 и |y| < = 3;
е) |х| > = и |y| < = 3.

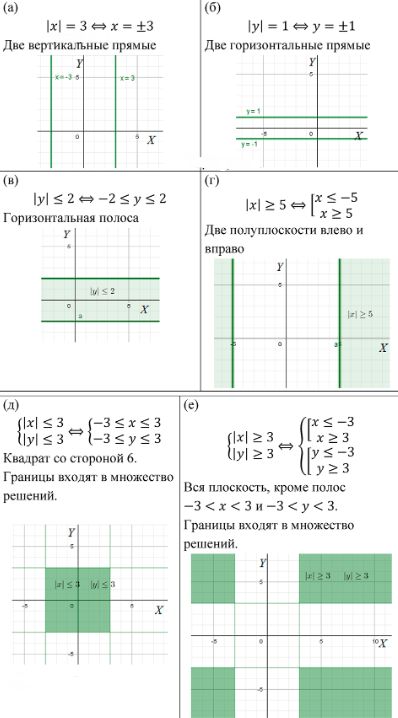
а) \( |x| = 3 \) — две вертикальные прямые, проходящие через точки \( x = 3 \) и \( x = -3 \).

б) \( |y| = 1 \) — две горизонтальные прямые, проходящие через точки \( y = 1 \) и \( y = -1 \).

в) \( |y| \leq 2 \) — область, расположенная между двумя горизонтальными прямыми \( y = 2 \) и \( y = -2 \), включая эти прямые.

г) \( |x| \geq 5 \) — две вертикальные прямые, проходящие через точки \( x = 5 \) и \( x = -5 \), включая эти прямые, а также все точки, расположенные за пределами этих прямых.

д) \( |x| \leq 3 \) и \( |y| \leq 3 \) — прямоугольная область, ограниченная прямыми \( x = 3 \), \( x = -3 \), \( y = 3 \) и \( y = -3 \), включая сами эти прямые.

е) \( |x| \geq 0 \) и \( |y| \leq 3 \) — область, расположенная между горизонтальными прямыми \( y = 3 \) и \( y = -3 \), и вертикальная область, начинающаяся от оси \( x \) и распространяющаяся в обе стороны от неё.

а) \( |x| = 3 \) — это две вертикальные прямые, проходящие через точки \( x = 3 \) и \( x = -3 \) на оси \( x \). Эти прямые включены в множество, так как \( |x| = 3 \) означает, что \( x \) может быть либо 3, либо -3. Все точки на этих прямых и точки, расположенные на их вертикальных линиях, удовлетворяют условию. Геометрически это означает, что мы имеем две вертикальные прямые, которые пересекают ось \( y \), но не образуют никакой области между ними — они просто задают положение на оси \( x \) для значений 3 и -3.

б) \( |y| = 1 \) — это две горизонтальные прямые, проходящие через точки \( y = 1 \) и \( y = -1 \) на оси \( y \). Эти прямые включены в множество, так как \( |y| = 1 \) означает, что \( y \) может быть либо 1, либо -1. Это выражение создаёт две линии, параллельные оси \( x \), которые ограничивают диапазоны значений по оси \( y \) на уровнях 1 и -1. Таким образом, все точки, расположенные вдоль этих двух прямых, удовлетворяют этому неравенству.

в) \( |y| \leq 2 \) — это область, расположенная между двумя горизонтальными прямыми \( y = 2 \) и \( y = -2 \), включая сами эти прямые. Все точки, для которых значение \( y \) лежит в пределах от -2 до 2, принадлежат данной области. Это означает, что мы имеем горизонтальный интервал, ограниченный прямыми \( y = 2 \) и \( y = -2 \), в пределах которого значение по оси \( y \) остаётся между этими двумя прямыми, и значения по оси \( x \) могут быть любыми.

г) \( |x| \geq 5 \) — это область, расположенная за пределами вертикальных прямых \( x = 5 \) и \( x = -5 \). Все точки, для которых значение \( x \) больше или равно 5, или меньше или равно -5, принадлежат этому множеству. Эти прямые образуют границу области, которая находится слева от \( x = -5 \) и справа от \( x = 5 \). Таким образом, вся область за пределами этих прямых, как слева, так и справа от этих линий, является частью решения. Все точки с координатами \( x \), которые лежат в этих областях, удовлетворяют условию \( |x| \geq 5 \).

д) \( |x| \leq 3 \) и \( |y| \leq 3 \) — это прямоугольная область, ограниченная прямыми \( x = 3 \), \( x = -3 \), \( y = 3 \) и \( y = -3 \), включая сами эти прямые. Все точки внутри этого прямоугольника, а также точки на его границах, удовлетворяют данному условию. Таким образом, мы имеем прямоугольник, расположенный в пределах координат \( x \in [-3, 3] \) и \( y \in [-3, 3] \), и включающий все точки внутри этого прямоугольника и на его границах. Это является основной областью для множества точек, которые могут иметь как положительные, так и отрицательные значения по обеим осям.

е) \( |x| \geq 0 \) и \( |y| \leq 3 \) — это область, расположенная между горизонтальными прямыми \( y = 3 \) и \( y = -3 \), и вертикальная область, начинающаяся от оси \( x \) и распространяющаяся в обе стороны от неё. Это означает, что все точки с положительными или нулевыми значениями по оси \( x \), а также значениями по оси \( y \), которые находятся между -3 и 3, принадлежат данной области. Графически, эта область охватывает верхнюю и нижнюю часть координатной плоскости, ограниченную горизонтальными прямыми, и области вдоль оси \( x \), где \( x \geq 0 \).