ГДЗ по Алгебре 7 Класс Номер 469 Дорофеев, Суворова — Подробные Ответы

Задача

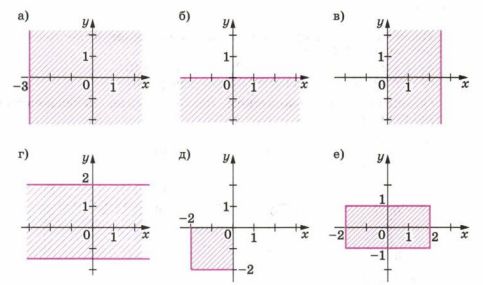
Опишите на алгебраическом языке области координатной плоскости, изображённые на рисунке 5.26, a—е.

Краткий ответ:

а) \( x > -3 \);

б) \( y \leq 0 \);

в) \( 0 < x \leq 2.5 \);

г) \( -1.5 \leq y \leq 2 \);

д) \( -2 \leq x \leq 0 \) и \( -2 \leq y \leq 0 \);

е) \( -2 \leq x \leq 2 \) и \( -1 \leq y \leq 1 \);

Подробный ответ:

а) \( x > -3 \) — это область на координатной плоскости, которая расположена справа от вертикальной прямой \( x = -3 \), но сама эта прямая не включена в область. Это означает, что все точки, у которых \( x \) больше -3, принадлежат этому множеству. Геометрически это полуплоскость, расположенная вправо от вертикальной прямой \( x = -3 \), не включая саму прямую. Область будет включать все точки, для которых значение по оси \( x \) больше -3, а \( y \) может принимать любые значения.

б) \( y \leq 0 \) — это область на координатной плоскости, которая расположена ниже горизонтальной прямой \( y = 0 \), включая саму прямую. Это означает, что все точки, у которых \( y \) меньше либо равно нулю, принадлежат этой области. Геометрически это полуплоскость, расположенная ниже оси \( x \), включая саму ось. В этой области значение по оси \( y \) будет отрицательным или равным нулю, а значение по оси \( x \) может быть любым.

в) \( 0 < x \leq 2.5 \) — это область на координатной плоскости, которая расположена между вертикальными прямыми \( x = 0 \) и \( x = 2.5 \). Эти прямые включены в область, так как неравенство \( \leq \) предполагает, что точка на прямой \( x = 2.5 \) также удовлетворяет условию. Таким образом, эта область включает все точки с координатами \( x \), которые находятся между 0 и 2.5, а значения по оси \( y \) могут быть любыми. Это прямоугольная область, расположенная между вертикальными прямыми и вдоль всей оси \( y \).

г) \( -1.5 \leq y \leq 2 \) — это область на координатной плоскости, которая ограничена двумя горизонтальными прямыми \( y = -1.5 \) и \( y = 2 \). Эти прямые включены в область, так как неравенства \( \leq \) и \( \geq \) позволяют точкам на этих прямых быть частью множества. Все точки, для которых значение \( y \) лежит между -1.5 и 2, а значение \( x \) может быть любым, принадлежат этой области. Это горизонтальная полоса, ограниченная прямыми на уровне \( y = -1.5 \) и \( y = 2 \).

д) \( -2 \leq x \leq 0 \) и \( -2 \leq y \leq 0 \) — это прямоугольная область, ограниченная прямыми \( x = -2 \), \( x = 0 \), \( y = -2 \) и \( y = 0 \). Эти прямые включены в область, так как неравенства \( \leq \) позволяют точки на этих прямых быть частью множества. Все точки, которые лежат между этими прямыми и для которых значения \( x \) лежат в пределах от -2 до 0, а значения \( y \) — от -2 до 0, принадлежат этой области. Это прямоугольник с вершинами в точках \( (-2, -2) \), \( (0, -2) \), \( (-2, 0) \) и \( (0, 0) \), включая все его внутренние точки и границы.

е) \( -2 \leq x \leq 2 \) и \( -1 \leq y \leq 1 \) — это область на координатной плоскости, ограниченная прямыми \( x = -2 \), \( x = 2 \), \( y = -1 \) и \( y = 1 \). Эти прямые включены в область, так как неравенства \( \leq \) и \( \geq \) предполагают, что точки на этих прямых также принадлежат множеству. Эта область является прямоугольником с вершинами в точках \( (-2, -1) \), \( (2, -1) \), \( (-2, 1) \) и \( (2, 1) \), включая все его внутренние точки и границы. Все точки внутри этой области удовлетворяют указанным условиям для \( x \) и \( y \).

Оцени решение