ГДЗ по Алгебре 7 Класс Номер 467 Дорофеев, Суворова — Подробные Ответы

Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют двойному неравенству:
а) -12 < = x < = 8;
б) 1,5 < у < 2;
в) -5,5 < = х < = -5;
г) -0,5 < = у < = 1,5.

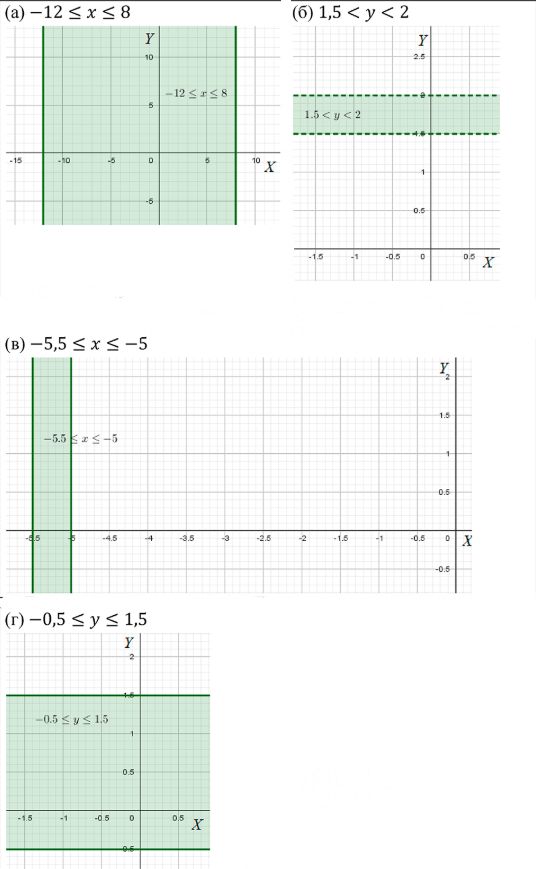
а) \( -12 \leq x \leq 8 \) — область, расположенная между двумя вертикальными прямыми \( x = -12 \) и \( x = 8 \), включая сами эти прямые.

б) \( 1.5 \leq y \leq 2 \) — область, расположенная между двумя горизонтальными прямыми \( y = 1.5 \) и \( y = 2 \), включая сами эти прямые.

в) \( -5.5 \leq x \leq -5 \) — область, расположенная между двумя вертикальными прямыми \( x = -5.5 \) и \( x = -5 \), включая сами эти прямые.

г) \( -0.5 \leq y \leq 1.5 \) — область, расположенная между двумя горизонтальными прямыми \( y = -0.5 \) и \( y = 1.5 \), включая сами эти прямые.

а) \( -12 \leq x \leq 8 \) — это область на координатной плоскости, которая ограничена двумя вертикальными прямыми: одна проходит через точку \( x = -12 \), а другая — через точку \( x = 8 \). Эти прямые включены в область, так как неравенство \( \leq \) предполагает, что точки на этих прямых также принадлежат множеству. Все точки, которые находятся между этими двумя прямыми, а также непосредственно на них, удовлетворяют данному условию. Таким образом, область, которая удовлетворяет условию \( -12 \leq x \leq 8 \), включает все точки, для которых значение координаты \( x \) лежит в пределах от -12 до 8.

б) \( 1.5 \leq y \leq 2 \) — это область, расположенная между двумя горизонтальными прямыми: одна проходит через точку \( y = 1.5 \), а другая — через точку \( y = 2 \). Эти прямые включены в область, так как неравенство \( \leq \) подразумевает, что точки на этих прямых также являются решениями. Все точки, расположенные между этими двумя прямыми, а также непосредственно на этих прямых, будут удовлетворять данному условию. Эта область охватывает все точки, для которых значение \( y \) лежит между 1.5 и 2, включая сами эти значения.

в) \( -5.5 \leq x \leq -5 \) — это область на координатной плоскости, ограниченная двумя вертикальными прямыми, проходящими через \( x = -5.5 \) и \( x = -5 \). Обе прямые включены в область, так как условие \( \leq \) включает сами эти прямые. Таким образом, эта область включает все точки, расположенные между прямыми \( x = -5.5 \) и \( x = -5 \), а также все точки на этих прямых, где значения координаты \( x \) лежат в пределах от -5.5 до -5.

г) \( -0.5 \leq y \leq 1.5 \) — это область, расположенная между двумя горизонтальными прямыми: одна проходит через точку \( y = -0.5 \), а другая — через точку \( y = 1.5 \). Эти прямые включены в область, так как неравенство \( \leq \) позволяет включать сами эти прямые. Все точки, расположенные между этими прямыми, а также непосредственно на этих прямых, будут удовлетворять данному условию. Таким образом, область, которая удовлетворяет условию \( -0.5 \leq y \leq 1.5 \), включает все точки, для которых значение \( y \) лежит в пределах от -0.5 до 1.5, включая сами эти значения.