ГДЗ по Алгебре 7 Класс Номер 462 Дорофеев, Суворова — Подробные Ответы

Изобразите на координатной плоскости множество точек, которое задаётся равенством:
а) х = 3;
б) х = -1,25;
в) у = -2;
г) у = 25;
д) х = 0;
е) у = 0.

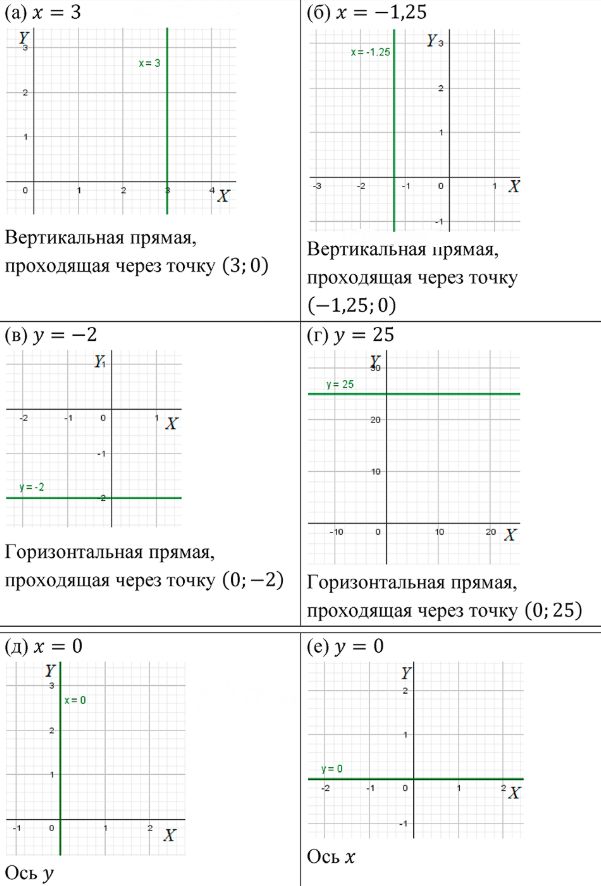
а) \( x = 3 \) — вертикальная прямая, проходящая через точку \( x = 3 \) на оси \( x \). Она будет параллельна оси \( y \).

б) \( x = -1.25 \) — вертикальная прямая, проходящая через точку \( x = -1.25 \) на оси \( x \), параллельная оси \( y \).

в) \( y = -2 \) — горизонтальная прямая, проходящая через точку \( y = -2 \) на оси \( y \). Она будет параллельна оси \( x \).

г) \( y = 25 \) — горизонтальная прямая, проходящая через точку \( y = 25 \) на оси \( y \), параллельная оси \( x \).

д) \( x = 0 \) — вертикальная прямая, проходящая через начало координат \( (0, 0) \) и параллельная оси \( y \), то есть это ось \( y \).

е) \( y = 0 \) — горизонтальная прямая, проходящая через начало координат \( (0, 0) \) и параллельная оси \( x \), то есть это ось \( x \).

а) \( x = 3 \) — это вертикальная прямая, которая проходит через точку \( x = 3 \) на оси \( x \). Она будет параллельна оси \( y \), что означает, что значение \( x \) будет постоянно равным 3 для всех точек этой прямой, но значение \( y \) может изменяться на любом отрезке, то есть она будет пересекать ось \( y \) в разных точках. Эта прямая не будет пересекать ось \( x \), так как она проходит только через все точки с \( x = 3 \), и её положение на оси \( y \) будет варьироваться.

б) \( x = -1.25 \) — это также вертикальная прямая, которая проходит через точку \( x = -1.25 \) на оси \( x \), и, как и предыдущая прямая, она будет параллельна оси \( y \). Это означает, что для всех точек этой прямой значение \( x \) всегда будет равно -1.25, в то время как значение \( y \) может изменяться. Такая прямая не пересекает ось \( x \), так как её \( x \)-координата фиксирована на уровне -1.25, и она не касается оси \( x \), только проходит вдоль оси \( y \) через этот пункт.

в) \( y = -2 \) — это горизонтальная прямая, которая проходит через точку \( y = -2 \) на оси \( y \). Эта линия будет параллельна оси \( x \), что означает, что для всех точек прямой значение \( y \) всегда будет равно -2, а значения \( x \) могут быть любыми. Эта прямая пересекает ось \( y \) в точке \( (0, -2) \) и будет проходить по всем точкам на оси \( x \), но её \( y \)-значение всегда останется постоянным —2. Она не пересекает ось \( x \), так как \( y \) остаётся неизменным.

г) \( y = 25 \) — это горизонтальная прямая, которая проходит через точку \( y = 25 \) на оси \( y \), и также будет параллельна оси \( x \). Это условие говорит, что для всех точек прямой значение \( y \) всегда равно 25, а \( x \)-координаты могут быть любыми. Эта прямая проходит на уровне \( y = 25 \) и будет продолжаться вправо и влево вдоль оси \( x \). Она не пересекает ось \( x \), потому что её значение по оси \( y \) всегда равно 25.

д) \( x = 0 \) — это вертикальная прямая, которая проходит через начало координат \( (0, 0) \) и параллельна оси \( y \). Она является осью \( y \), поскольку проходит вдоль всей оси \( y \), и все точки этой прямой имеют значение \( x = 0 \), а \( y \)-координаты могут быть любыми. Эта прямая делит координатную плоскость на две части: положительные и отрицательные значения \( y \), и её положения на оси \( x \) всегда будут равны 0.

е) \( y = 0 \) — это горизонтальная прямая, которая также проходит через начало координат \( (0, 0) \) и параллельна оси \( x \). Это ось \( x \), которая проходит по всем точкам на оси \( x \), где значение \( y = 0 \). Все точки, лежащие на оси \( x \), имеют нулевое значение по оси \( y \), и эта прямая делит координатную плоскость на положительные и отрицательные значения \( x \). Эта прямая не пересекает ось \( y \), так как её значение по оси \( y \) всегда равно 0.