ГДЗ по Алгебре 7 Класс Номер 458 Дорофеев, Суворова — Подробные Ответы
Изобразите на координатной прямой множество точек, координаты которых удовлетворяют условию:
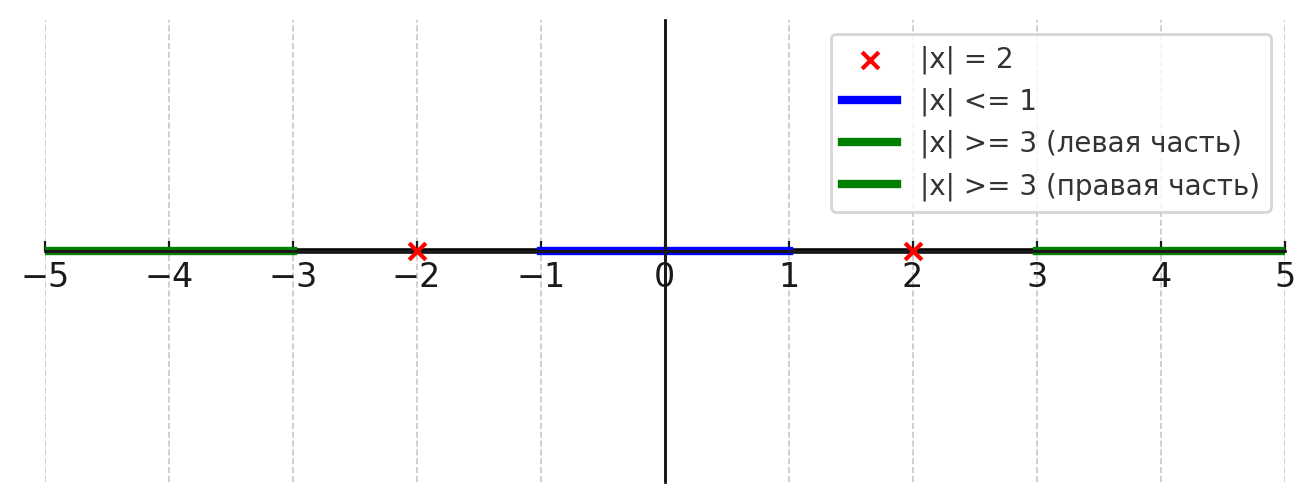
а) |x| = 2;
б) |x| < =1;
в) |x| > = 3.
Подсказка. Прочитайте данное условие, используя слово «расстояние», например: |x| = 6 — расстояние от точки х до 0 равно 6.
1) Условие: \( |x| = 2 \)
Это означает, что расстояние от точки \( x \) до нуля равно 2. То есть, \( x \) может быть либо 2, либо -2.
Множество точек: \( \{ -2, 2 \} \).
2) Условие: \( |x| \leq 1 \)
Это означает, что расстояние от точки \( x \) до нуля не больше 1. Таким образом, \( x \) может быть любым значением на отрезке от -1 до 1, включая границы.
Множество точек: \( [-1, 1] \).
3) Условие: \( |x| \geq 3 \)
Это означает, что расстояние от точки \( x \) до нуля больше либо равно 3. То есть, \( x \) может быть либо меньше или равно -3, либо больше или равно 3.
Множество точек: \( (-\infty, -3] \cup [3, +\infty) \).
1) Условие: \( |x| = 2 \)
Это условие говорит, что расстояние от точки \( x \) до нуля на координатной прямой должно быть ровно 2 единицы. Это означает, что существует два возможных значения для \( x \), которые удовлетворяют этому условию. Одно из них — это 2, а другое — это -2, так как оба значения имеют расстояние 2 от нуля. Следовательно, множество точек, которые удовлетворяют этому условию, состоит из двух элементов: \( -2 \) и \( 2 \).
Множество точек, удовлетворяющих условию \( |x| = 2 \): \( \{ -2, 2 \} \).
2) Условие: \( |x| \leq 1 \)
Это условие подразумевает, что расстояние от точки \( x \) до нуля не должно превышать 1. В этом случае \( x \) может быть любым значением, находящимся на отрезке от -1 до 1, включая эти два числа, так как они точно соответствуют условию. То есть, возможные значения \( x \) варьируются от \( -1 \) до \( 1 \), включительно. Множество точек, которое соответствует этому условию, включает все значения на этом отрезке, и его можно выразить как интервал от \( -1 \) до \( 1 \), где обе границы включены.
Множество точек, удовлетворяющих условию \( |x| \leq 1 \): \( [-1, 1] \).
3) Условие: \( |x| \geq 3 \)
Это условие говорит, что расстояние от точки \( x \) до нуля должно быть не меньше 3. Таким образом, точки, которые удовлетворяют этому условию, могут быть либо больше или равно 3, либо меньше или равно -3. Это означает, что возможные значения \( x \) могут лежать в двух областях: одна область — это все значения, которые меньше или равны -3, а другая — это все значения, которые больше или равны 3. Поэтому множество точек, удовлетворяющих условию \( |x| \geq 3 \), состоит из двух частей: полуинтервалов \( (-\infty, -3] \) и \( [3, +\infty) \).
Множество точек, удовлетворяющих условию \( |x| \geq 3 \): \( (-\infty, -3] \cup [3, +\infty) \).