ГДЗ по Алгебре 7 Класс Номер 457 Дорофеев, Суворова — Подробные Ответы
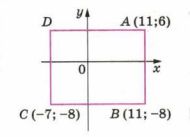
Четырёхугольник ABCD, изображённый на рисунке 5.16, является прямоугольником. Найдите периметр этого прямоугольника.
1) AD = BC = \( |11 — (-7)| = |18| = 18 \).
2) CD = AB = \( |6 — (-8)| = |14| = 14 \).
3) Периметр равен:
\( 2 \cdot (18 + 14) = 2 \cdot 32 = 64 \).
Ответ: 64.
1) Рассчитаем длину отрезка AD и BC, используя координаты точек на числовой прямой. Для этого воспользуемся формулой для вычисления расстояния между двумя точками. В данном случае у нас есть координаты точек A(–7) и D(11), а также B(–7) и C(11). Мы можем выразить длину отрезка как модуль разности координат этих точек:
\( AD = |11 — (-7)| = |11 + 7| = |18| = 18 \).
Это означает, что расстояние между точками A и D, а также между точками B и C равно 18.
2) Теперь вычислим длину отрезка CD и AB. Мы будем использовать те же принципы. Для отрезков CD и AB у нас есть следующие координаты точек: C(–8) и D(6), а также A(–8) и B(6). Таким образом, длина отрезка CD и AB будет:
\( CD = AB = |6 — (-8)| = |6 + 8| = |14| = 14 \).
Это значит, что расстояние между точками C и D, а также между точками A и B равно 14.
3) Для нахождения периметра нужно сложить все длины отрезков, образующих периметр, и умножить на 2, так как у нас прямоугольник. Мы уже нашли длины отрезков AD, BC, CD и AB, которые составляют стороны прямоугольника. Эти длины составляют 18 и 14:
Периметр прямоугольника равен:
\( 2 \cdot (18 + 14) = 2 \cdot 32 = 64 \).
Ответ: периметр прямоугольника равен 64.
Ответ: 64.