ГДЗ по Алгебре 7 Класс Номер 449 Дорофеев, Суворова — Подробные Ответы

Задача

Изобразите на координатной прямой указанные промежутки (используйте для этого разные цветные карандаши). Найдите объединение и пересечение этих промежутков:
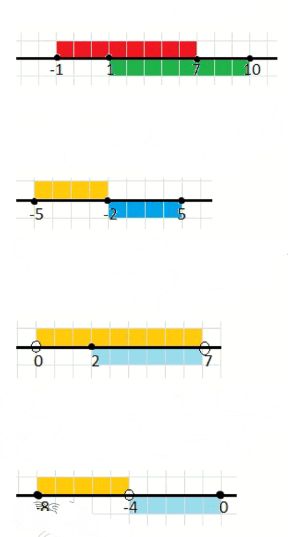
а) -1 < = x < = 7, 1 < =x < =10;
б) -5 < = х < = -2, -2 < = x < = 5;
в) 0 < х < 7, 2 < = х < = 7;
г) -8 < = х < -4, -4 < x < = 0.

Краткий ответ:

а)
Промежуток -1 ≤ x ≤ 7: от -1 до 7, включая обе границы.
Промежуток 1 ≤ x ≤ 10: от 1 до 10, включая обе границы.
Объединение этих двух промежутков: от -1 до 10, включая обе границы.
Пересечение: от 1 до 7, включая обе границы.

б)
Промежуток -5 ≤ x ≤ -2: от -5 до -2, включая обе границы.
Промежуток -2 ≤ x ≤ 5: от -2 до 5, включая обе границы.
Объединение: от -5 до 5, включая обе границы.
Пересечение: от -2 до -2 (в точности x = -2).

в)
Промежуток 0 < x < 7: от 0 до 7, не включая 0 и 7.
Промежуток 2 ≤ x ≤ 7: от 2 до 7, включая 2 и 7.
Объединение: от 0 до 7, включая 7, но не включая 0.
Пересечение: от 2 до 7, включая обе границы.

г)
Промежуток -8 ≤ x < -4: от -8 до -4, включая -8, но не включая -4.
Промежуток -4 < x ≤ 0: от -4 до 0, не включая -4, но включая 0.

Подробный ответ:

а)
Промежуток -1 ≤ x ≤ 7: этот промежуток включает все значения от -1 до 7, включая как саму точку -1, так и точку 7. То есть, любые значения \( x \) такие, что \( x \) лежит в этом диапазоне, будут удовлетворять условию. Графически это будет отрезок на координатной прямой, включающий оба конца.
Промежуток 1 ≤ x ≤ 10: аналогично, этот промежуток включает все значения от 1 до 10, включая обе границы, 1 и 10. Графически это также будет отрезок на прямой, включающий оба конца.
Объединение этих двух промежутков: объединение двух промежутков включает все значения, которые принадлежат хотя бы одному из этих промежутков. Графически это будет отрезок от -1 до 10, включающий оба конца. То есть, значения \( x \), лежащие в пределах от -1 до 10, удовлетворяют хотя бы одному из двух условий. Таким образом, объединение этих двух промежутков будет отрезком от -1 до 10, включая обе границы.
Пересечение этих двух промежутков: пересечение включает только те значения, которые одновременно принадлежат обоим промежуткам. Так как первый промежуток включает все значения от -1 до 7, а второй промежуток включает все значения от 1 до 10, пересечением этих двух промежутков будет отрезок от 1 до 7, включая обе границы. Таким образом, пересечение этих промежутков будет отрезком от 1 до 7, также включая обе границы.

б)
Промежуток -5 ≤ x ≤ -2: данный промежуток включает все значения от -5 до -2, включая оба конца, то есть значения \( x \), которые лежат в диапазоне от -5 до -2, включают и сами точки -5 и -2. Этот промежуток представляет собой отрезок на координатной прямой.
Промежуток -2 ≤ x ≤ 5: аналогично, этот промежуток включает все значения от -2 до 5, включая обе границы. Значения \( x \), которые лежат в этом промежутке, будут удовлетворять условию, включая точки -2 и 5.
Объединение этих двух промежутков: объединение двух промежутков включает все значения, которые принадлежат хотя бы одному из этих промежутков. Таким образом, объединение двух промежутков будет отрезком от -5 до 5, включая обе границы. Это объясняется тем, что первый промежуток начинается с -5 и заканчивается на -2, а второй промежуток начинается с -2 и продолжается до 5, то есть все значения от -5 до 5 будут включены в объединение.
Пересечение этих двух промежутков: пересечение включает те значения, которые одновременно принадлежат обоим промежуткам. Поскольку оба промежутка включают точку -2, пересечение будет содержать только одну точку -2, так как это единственное значение, которое лежит в обоих промежутках. Таким образом, пересечение этих двух промежутков будет точкой \( x = -2 \).

в)
Промежуток 0 < x < 7: этот промежуток включает все значения от 0 до 7, за исключением самих точек 0 и 7. То есть, значения \( x \), которые принадлежат этому промежутку, не могут быть равны ни 0, ни 7, но могут быть любыми числами между ними. Графически это будет открытый отрезок, не включая концы.
Промежуток 2 ≤ x ≤ 7: данный промежуток включает все значения от 2 до 7, включая обе границы, то есть значения \( x \), которые лежат в этом диапазоне, могут быть равны как 2, так и 7. Этот промежуток также будет отрезком на координатной прямой.
Объединение этих двух промежутков: объединение включает все значения, которые принадлежат хотя бы одному из этих промежутков. В данном случае объединение будет включать значения от 0 до 7, но не включая 0, так как это значение не входит в первый промежуток, и включая 7, так как это значение входит во второй промежуток. Таким образом, объединение этих двух промежутков будет отрезком от 0 до 7, не включая 0, но включая 7.
Пересечение этих двух промежутков: пересечение включает те значения, которые одновременно принадлежат обоим промежуткам. Таким образом, пересечением будет отрезок от 2 до 7, включая обе границы. Это объясняется тем, что первый промежуток не включает 2, а второй промежуток включает, и оба промежутка заканчиваются на 7.

г)
Промежуток -8 ≤ x < -4: этот промежуток включает все значения от -8 до -4, включая точку -8, но не включая -4. То есть, значения \( x \), которые лежат в этом диапазоне, могут быть равны -8, но не могут быть равны -4. Графически это будет отрезок на координатной прямой, не включая конец -4.
Промежуток -4 < x ≤ 0: данный промежуток включает все значения от -4 до 0, не включая -4, но включая 0. То есть, значения \( x \), которые лежат в этом промежутке, могут быть равны 0, но не могут быть равны -4.
Объединение этих двух промежутков: объединение включает все значения, которые принадлежат хотя бы одному из этих промежутков. В данном случае объединение будет включать все значения от -8 до 0, не включая -8, но включая 0. Это объясняется тем, что первый промежуток начинается с -8 и не включает -4, а второй промежуток начинается с -4 и продолжается до 0, включая 0. Таким образом, объединение будет отрезком от -8 до 0, включая 0 и не включая -8.
Пересечение этих двух промежутков: пересечение включает те значения, которые одновременно принадлежат обоим промежуткам. Так как оба промежутка не включают -4, пересечением будет только точка -4, которая не входит ни в один из промежутков. Таким образом, пересечение этих промежутков состоит только из точки \( x = -4 \).

Оцени решение