ГДЗ по Алгебре 7 Класс Номер 448 Дорофеев, Суворова — Подробные Ответы

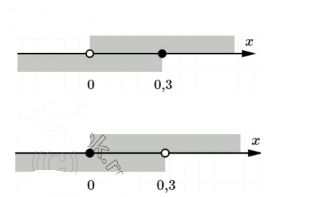
Запишите с помощью двойных неравенств и изобразите на координатной прямой полуинтервалы от точки 0 до точки 0,3. Сколько существует таких полуинтервалов?

Полуинтервалы с разными границами

Полуинтервал с левой границей (включённой), но правой (не включённой):

Это выражается неравенством:
0 ≤ x < 0,3

То есть, x может быть любым значением от 0 до 0,3, но 0,3 не включается.

Полуинтервал с правой границей (включённой), но левой (не включённой):

Это выражается неравенством:
0 < x ≤ 0,3

То есть, x может быть любым значением от 0 (но не включая 0) до 0,3, и 0,3 включается.

Полуинтервалы с разными типами границ

Полуинтервал с левой границей (включённой), но правой (не включённой):

Этот полуинтервал обозначает, что точка на координатной прямой может быть как 0, так и любое значение, большее 0, но меньшее 0,3. Точка 0 включена в полуинтервал, но точка 0,3 — нет. Таким образом, полуинтервал содержит все значения от 0 до 0,3, исключая саму точку 0,3.
Неравенство, описывающее данный полуинтервал:
0 ≤ x < 0,3

Для этого полуинтервала важна следующая особенность: когда точка лежит на границе с левой стороны (включена), но на правой границе (0,3) она не присутствует. Это означает, что \( x \) может принимать любые значения внутри интервала, но не может быть равным 0,3. Например, \( x = 0 \) или \( x = 0,2 \) — оба этих значения принадлежат полуинтервалу, а вот \( x = 0,3 \) уже нет.

Полуинтервал с правой границей (включённой), но левой (не включённой):

Этот полуинтервал описывает ситуацию, когда точка на координатной прямой не может быть равной 0, но может быть любым значением больше 0 и до 0,3, включая 0,3. То есть, в этом полуинтервале включена правая граница, но не включена левая. Это означает, что значение 0 исключено, а 0,3 — включено.
Неравенство, описывающее данный полуинтервал:
0 < x ≤ 0,3

Важной особенностью данного полуинтервала является то, что точка 0 исключена, и все значения от 0 до 0,3 (включая 0,3) считаются допустимыми. Например, если \( x = 0,1 \) или \( x = 0,2 \), то эти значения принадлежат полуинтервалу. Но если \( x = 0 \), то оно не принадлежит этому полуинтервалу, так как 0 в нём не включено.

Таким образом, каждый из этих полуинтервалов имеет свои особенности, связанные с включением или исключением границ. Эти различия важны, так как определяют, какие именно числа могут быть частью каждого полуинтервала. Суть полуинтервала в том, чтобы ограничить диапазон значений с одной или обеими границами, причем одна из границ может быть включена, а другая — нет, в зависимости от типа полуинтервала.